O átomo de hidrogênio é composto por um próton no núcleo e um elétron, que se move ao redor do núcleo. Na teoria quântica de estrutura atômica supõe-se que o elétron não se mova em uma órbita bem definida. Ao contrário, ele ocupa um estado conhecido como , que pode ser pensado como uma “nuvem” de carga negativa rodeando o núcleo. No estado de energia mais baixa, chamado , ou , é suposto que o formato do orbital seja uma esfera com centro no núcleo. Essa esfera é descrita em termos da função densidade de probabilidade
onde é o . A integral
dá a probabilidade de o elétron ser encontrado dentro da esfera de raio metros centrada no núcleo.
- Verifique se é uma função densidade de probabilidade.
- Encontre Para que valor de a função tem seu valor máximo?
- Desenhe a função densidade.
- Calcule a probabilidade de o elétron estar dentro da esfera de raio centrada no núcleo.
- Calcule a distância média do elétron e do núcleo no estado fundamental do átomo de hidrogênio.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente verificar que a função , se é uma função densidade de probabilidade. Depois, encontrar o Para que valor de a função tem seu valor máximo, desenhar a função densidade, calcular a probabilidade de o elétron estar dentro da esfera de raio centrada no núcleo e calcular a a distância média do elétron e do núcleo no estado fundamental do átomo de hidrogênio.
Em geral, a função densidade de probabilidade de uma variável aleatória satisfaz para todo . Além disso, como as probabilidades são medidas em uma escala de até , segue que:
Então, o que precisamos fazer é provar que é maior ou igual a zero para todo e verificar se a integral da função de a vai dar . Depois, calculamos o limite que o enunciado nos pede, esboçamos o gráfico da função e calculamos a probabilidade no intervalo , usando a fórmula:
Vamos lá!
Passo 2
A questão já nos diz que para . isso significa que ela vai ser sempre maior ou igual a zero para todo , ou seja:
Agora vamos verificar a segunda condição, calculando a integral:
Substituindo e a condição (que representa o intervalo ), temos:
Isso nos dá uma integral imprópria, que pode ser escrita na forma do limite:
Usando integração por partes, um sistema de computação algébrico, (ou dando aquela olhadinha no Exercício 18), a gente tem que:
Agora a gente usa com e aplica a regra de L’Hopital para obter:
Isso satisfaz a segunda condição para a função ser uma função densidade de probabilidade.
Passo 3
Agora vamos (b) calcular o para que valor de da função tenha seu valor máximo:
Assim, usando L’Hopital, temos que:
Simplificando:
E calculando o limite, obtemos:
Para encontrar o máximo de , nós derivamos a função:
Igualando a zero, temos:
Ou
muda de positivo para negativo em , então tem um valor máximo em .
Passo 4
(c) É bastante difícil desenhar um retângulo de visualização dessa função, mas como a gente já conhece um ponto máximo, encontrado na parte (b), isso facilita muito!
Assim, temos que:
Com um máximo perto de milhões, e uma área total sob a curva que vale , representando a probabilidade total, nós sabemos que a “corcunda” dessa curva no gráfico deve ser extremamente limitada.
Assim, obtemos o seguinte esboço:
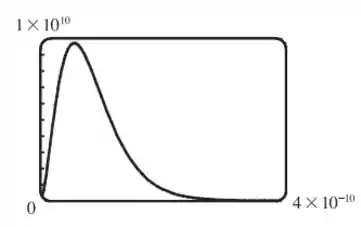
Passo 5
(d) Calculando a probabilidade, usando a fórmula do passo , temos:
Usando o da parte (a), com , temos:
Aplicando o intervalo de integração:
E simplificando:
Passo 6
(e) Agora para calcular a distância média, vamos usar a fórmula:
Assim, substituindo os dados da nossa função, temos:
Integrando por partes três vezes ou usando algum sistema de computação algébrica, nós temos que :
Assim, com e usando L’Hopital, nós obtemos:
Valeu, galera! Até a próxima! 😉
Resposta
(a) A função é uma função densidade de probabilidade.
(b)
(c) Gráfico
(d)
(e)