Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.3 - Ex. 64

(a)

Use a parte (c) do Exercício 50 na Seção 0.4 e a regra da cadeia para mostrar que

d d x [ a r c csc ⁡ x ] =   - 1 x x 2 - 1    

Com x > 1

(b)

Conclua da parte (a) que

d d u [ a r c csc ⁡ u ] =   - 1 u u 2 - 1     d u d x

Com u > 1

(c)

Use a equação (11) da Seção 0.4 e as partes (b) e (c) do Exercício 50 daquela seção para mostrar que, se | x |   ≥   1 , então a r c s e c   x   +   a r c   c o s s e c   x   =   π / 2 . Conclua da parte (a) que

d d x [ a r c sec ⁡ x ] =   1 x x 2 - 1    

(d)

Conclua da parte(c) que

d d u [ a r c sec ⁡ u ] =   1 u u 2 - 1     d u d x

Passo 1

A parte (c) do Exercício 50 na Seção 0.4 diz basicamente que:

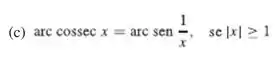
Como a questão já fala que x > 1 , podemos usar essa relação. Se derivarmos ela fica assim:

d d x [ a r c csc ⁡ x ] = d d x [ a r c sin ⁡ 1 x ]

Mas se puxarmos da memória vamos lembrar que:

d d x a r c sin ⁡ u = 1 1 - u 2     d u d x

Então vamos chegar que:

d d x a r c csc ⁡ x = d d x a r c sin ⁡ 1 x =   1 1 - 1 x 2       1 x '

d d x a r c csc ⁡ x = 1 x 2 - 1 x 2     - 1 2 x 2

Quando esse x 2 sai da raiz ele terá que sair como x

d d x a r c csc ⁡ x =   x x 2 - 1     - 1 x 2

Opa então olha só aonde vamos chegar, exatamente o que queríamos mostrar:

d d x a r c csc ⁡ x =   - 1 x x 2 - 1    

Passo 2

(b)

Sendo u uma função de x , basta aplicarmos a regra da cadeia em d d x a r c csc ⁡ x , usando o resultado da letra (a) chegaremos que

d d u [ a r c csc ⁡ u ] =   - 1 u u 2 - 1     d u d x

Pra x > 1

Passo 3

(c)

A equação (11) da Seção 0.4 diz basicamente que

E as partes (b) e (c) do Exercício 50 dizem que:

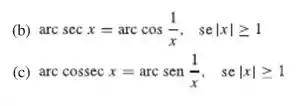
Podemos isolar chamar u = 1 x , ficaremos que

  a r c sin ⁡ u   = a r c csc ⁡ 1 u

a r c cos ⁡ u = a r c sec ⁡ 1 u

Como o Como a questão já fala que x ≥ 1 . Se substituirmos os valores de a r c sin ⁡ x   e   a r c cos ⁡ x da equação (11) pelas partes (b) e (c) do exercício 50, teremos que:

a r c sin ⁡ x + a r c cos ⁡ x = π 2

Substituindo:

a r c csc ⁡ 1 x + a r c sec ⁡ 1 x = π 2

Porém lembra que:

a r c csc ⁡ 1 x = a r c sec ⁡   x                         e                         a r c sec ⁡ x = a r c csc ⁡ 1 x

Então

a r c s e c   x   +   a r c   c o s s e c   x   =   π / 2

Passo 4

Usando essa expressão podemos falar que:

arc sec ⁡ x = π 2 - a r c csc ⁡ x  

Derivando em relação a x

d d x [ arc sec ⁡ x ] = d d x π 2 - a r c csc ⁡ x = d d x π 2 - d d x a r c csc ⁡ x

Como π / 2 é uma constante sua derivada é 0 . Então:

d d x [ arc sec ⁡ x ] = - d d x a r c csc ⁡ x

Usando o resultado da letra (a) chegamos que:

d d x [ arc sec ⁡ x ] = 1 x x 2 - 1    

Passo 5

(d)

Sendo u uma função de x , basta aplicarmos a regra da cadeia em d d x a r c sec ⁡ x , usando o resultado da letra (c) chegaremos que

d d u [ a r c sec ⁡ u ] =   1 u u 2 - 1     d u d x

Pra x ≥ 1

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja f x = s e nx . Encontre todos os inteiros positivos n com os quais f n x = s e nx .
Use o Método de Newton para aproximar a menor solução positiva de sen ⁡ x + cos ⁡ x = 0 .
30-a) Use recurso gráfico para fazer estimativas rudimentares dos pontos no intervalo [ 0,2 π ] nos quais o gráfico de y = s e nx cos ⁡ x tem uma reta tangente horizontal.b) Encontre a exata localizaç
Em cada parte, explique o que acontece se aplicarmos o Método de Newton a uma função f quando a condição dada é satisfeita para algum valor de n . f x n = 0 x n + 1 = x n x n + 2 = x n ≠ x n + 1
Encontre f ' x . f x = x 2 + 1c o t gx 3 - cos ⁡ x c o s s e cx