Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.5 - Ex. 30

30-a) Use recurso gráfico para fazer estimativas rudimentares dos pontos no intervalo [ 0,2 π ] nos quais o gráfico de y = s e n   x cos ⁡ x tem uma reta tangente horizontal.

b) Encontre a exata localização dos pontos onde o gráfico tem uma reta tangente horizontal.

Passo 1

a)

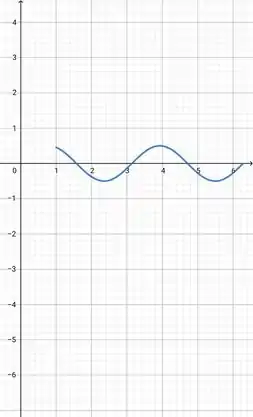
Pelo gráfico nós percebemos que os pontos para os quais a função tem uma reta tangente são para x = 1 , x = 2,5 , x = 4 , x = 5,5 .

Tranquilo, né ?

Passo 2

b) Galera, para resolvermos esse item nós devemos achar a derivada da função e igualar ela à zero. Ok ?

Então, vamos lá!

y ´ = cos 2 ⁡ x - s e n 2 x

Igualando a derivada à zero:

cos 2 ⁡ x - s e n 2 x = 0

cos 2 ⁡ x = s e n 2 x

cos ⁡ x = ±   s e n   x  

Bom isso quer dizer que nós temos que lembrar para quais ângulo temos cos ⁡ x = s e n   x   ou cos ⁡ x = - s e n   x .   Claro que dentro do intervalo de [ 0,2 π ] .

Para cos ⁡ x = s e n   x   , eu lembrei de   π 4 , e vocêss ??? Ahh e também tem 5 π 4 .

Para cos ⁡ x = - s e n   x   , temos:

x =   3 π 4   e   x = 7 π 4

Resposta

a) x = 1 , x = 2,5 , x = 4 , x = 5,5 .

b) x =   π 4 , x =   5 π 4 , x =   3 π 4 , x = 7   π 4 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre d y d x : y = x 2 ( a r cs e nx ) 3
Encontre d y d x : y = a r c sec ⁡ x + a r cc o s s e c ( x )
Encontre d y d x : y = a r c cssec ⁡ e x
Encontre d y d x : y = e x a r c sec ⁡ ( x )
28- a) Mostre que y = c o sx e y = s e nx são soluções da equação y ' ' + y = 0 . b) Mostre que y =As e nx + Bc o sx é uma solução da equação y ' ' + y = 0 para qualquer valor das constantes A e B .