Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 7.1 - Ex. 37

Avalie a integral indefinida. Ilustre e verifique se a sua resposta é razoável usando o gráfico da função e de sua antiderivada (C=0).

∫ x cos ⁡ π x d x

Passo 1

A resolução dessa integral tem duas partes! É preciso calma e paciência pra resolvê-lo. Vamos lá!

Para solucionarmos uma integral por partes, temos a seguinte fórmula:

∫ u d v = u v - ∫ v d u

O problema já nos dá o valor de u e d v , basta calcularmos a derivada e a integral, respectivamente:

u = x                               ;                 d u = d x

d v = cos ⁡ π x d x                 ;                       v = 1 π sin ⁡ π x

Assim, podemos substituir!!

Passo 2

Calculando a integral, temos

∫ u d v = u v - ∫ v d u

∫ x cos ⁡ π x d x = 1 π x sin ⁡ π x - ∫ 1 π sin ⁡ π x d x

Organizando...

∫ x cos ⁡ π x d x   = 1 π x sin ⁡ π x - 1 π ∫   sin ⁡ π x d x

Sabendo que ∫ sin ⁡ π x d x = - 1 π cos  ⁡ π x , então

∫ x cos ⁡ π x d x   = 1 π x sin ⁡ π x + 1 π ( 1 π cos  ⁡ π x )

Logo,

∫ x cos ⁡ π x d x   = 1 π x sin ⁡ π x + 1 π 2 cos ⁡ π x + C

Fazendo o gráfico, vemos que isso é razoável, uma vez que a função F (representado pela cor preta) tem valores extremos onde f é 0.

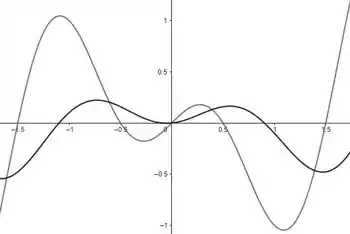
Showw né?!!

Resposta

∫ x cos ⁡ π x d x   = 1 π x sin ⁡ π x + 1 π 2 cos ⁡ π x + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral indefinida. ∫ arctan ⁡ xd x
Calcule a integral indefinida: ∫ ln ⁡ x d x
Calcule a integral indefinida: ∫ x 3 x d x
Calcule a integral indefinida: ∫ x cos ⁡ 2 x d x
Calcule a integral indefinida: ∫ sen - 1 ⁡ w d w