Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 5.2 - Ex. 35

Calcule a integral interpretando-a em termo das áreas.

∫ 0 3 1 2 x - 1 d x

Passo 1

Uma integral pode ser interpretada como a área entre a curva da função e o eixo x , considerando a área abaixo do eixo como negativa. Sendo A 1 a área acima do eixo x e A 2 a área abaixo, temos que a integral é calculada por:

A = A 1 - A 2

Vamos então esboçar o gráfico da função, calcular as áreas acima e abaixo do eixo e com isso obter o valor da integral.

Passo 2

Nossa função é f x = 1 2 x - 1 , uma reta. Temos nos extremos do intervalo de integração f 0 = - 1 e f 3 = 3 2 - 1 = 1 2 . A função passa pelo eixo x quando y = 0 :

1 2 x - 1 = 0 ⇒ 1 2 x = 1 ⇒ x = 2

Entao desenhamos a funcao e a área entre ela e o eixo:

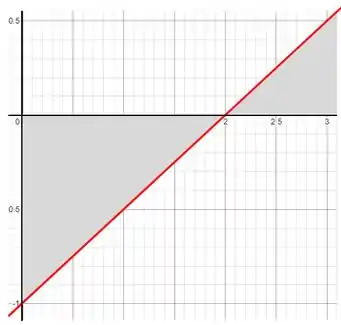
Passo 3

Só falta agora calcularmos a integral pela área dos triângulos. A área abaixo do gráfico que vai ser considerada negativa tem o seguinte valor:

A 2 = 1 ⋅ 2 2 = 1

A area acima do gráfico é:

A 1 = 1 ⋅ 0,5 2 = 0,25

Entao a integral fica:

∫ 0 3 1 2 x - 1 d x = A = A 1 - A 2 = 0,25 - 1 = - 0,75

Resposta

∫ 0 3 1 2 x - 1 d x = - 0,75

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a região limitada pelas curvas dadas. Decida quando integrar em relação a x ou a y. Desenhe um retângulo típico de aproximação e coloque sua altura e largura. Entao calcule a área da região.17.
Esboce a região limitada pelas curvas dadas. Decida quando integrar em relação a x ou a y. Desenhe um retângulo típico de aproximação e coloque sua altura e largura. Entao calcule a área da região.26.
Esboce a região limitada pelas curvas dadas. Decida quando integrar em relação a x ou a y. Desenhe um retângulo típico de aproximação e coloque sua altura e largura. Entao calcule a área da região.22.
Esboce a região limitada pelas curvas dadas. Decida quando integrar em relação a x ou a y. Desenhe um retângulo típico de aproximação e coloque sua altura e largura. Entao calcule a área da região.23.
Esboce a região limitada pelas curvas dadas. Decida quando integrar em relação a x ou a y. Desenhe um retângulo típico de aproximação e coloque sua altura e largura. Entao calcule a área da região.12.