Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.1 - Ex. 7
Avalie as somas superiores e inferiores para com e . Ilustre com diagramas como na figura 14.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente avaliar as somas superiores e inferiores para
No intervalo , com e . E ilustrar tudo isso com o diagrama da figura 14.
Tem ideia de como fazemos isso?
Para a gente fazer essa soma, temos que dividir a área abaixo da curva da função no intervalo em retângulos. Para as somas superiores, a altura de cada retângulo é dada a partir do maior valor possivel de e para as somas inferiores a altura é dada pelo menos valor possível.
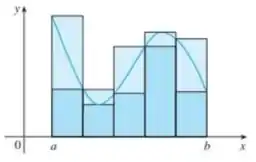
A área da região que está sob o gráfico de uma função contínua é o limite da soma das áreas dos retângulos aproximantes:
Onde e deve ser obtido analisando o gráfico da curva.
Sendo assim, vamos substituir os dados da função na fórmula do somatório e estimar a área sob o gráfico.
Vamos lá!
Passo 2
Perceba que da nossa fórmula e . Dessa forma, temos:
Vamos fazer o primeiro caso, ou seja, quando . Daí,
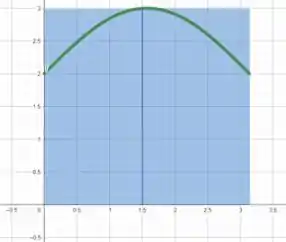
Perceba que o máximo valor de em ambos os subintervalos ocorre em .
Então a soma superior é:
Substituindo os valores através de temos:
Perceba também que o valor mínimo de nos subintervalos ocorre em e então, a soma inferior será dada por:
Substituindo os valores através de , temos:
Desenhando o diagrama para (dois retângulos), temos:
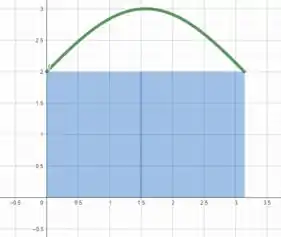
Tranquilo até aqui?
Passo 3
Faremos agora para . Então,
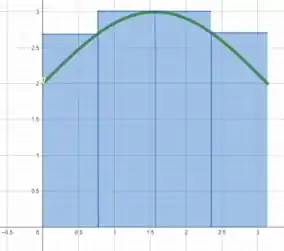
Dessa forma, a soma superior é:
Substituindo os valores através de temos:
Fazendo essa soma:
Agora para a soma inferior, vamos ter:
Substituindo os valores através de temos:
E calculando:
Desenhando o diagrama para , teremos:
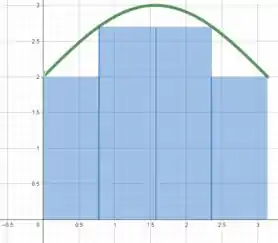
Show?
Passo 4
Faremos, agora para Daí,
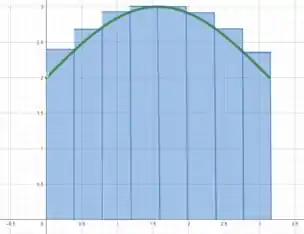
Dessa forma, temos que a soma superior é:
Substituindo os valores através de temos:
E nossa soma inferior será dada por:
Fazendo o diagrama para , temos:
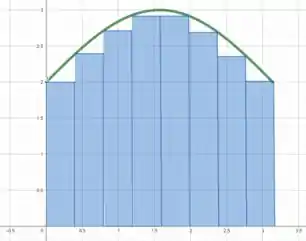
Valeu, galera! Até a próxima! 😉
Resposta
Sendo = Soma superior e = soma inferior, temos que
-Para e
-Para e
-Para e