Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.2 - Ex. 6a

  1. É dado o gráfico de uma função f .Estime ∫ - 2 4 f x d x   usando seis subintervalos com Extremidades direitas.

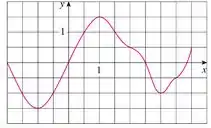
Passo 1

O enunciado nos da um gráfico da função f e nos pede pra estimar ∫ - 2 4 f x d x   usando seis subintervalos com extremidades direitas:

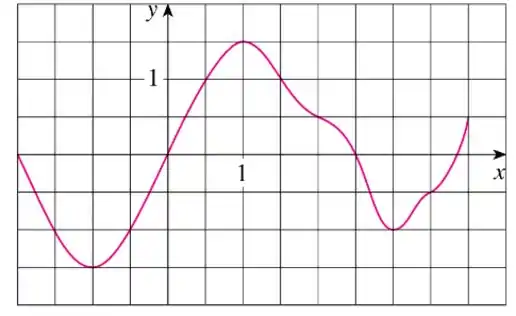
Para começar, vamos rever a fórmula da soma de Rieman:

S =   ∑ i = 1 4 f x i * Δ x    

Onde:

Δ x = b - a n .

Passo 2

Como precisamos das extremidades direitas, x i = a + i Δ x . Daí, temos que :

Δ x = b - a n = 4 - ( - 2 ) 6 = 1  

E,   x i = - 2 + i . Logo, nossa extremidades direita são x 1 = - 1 ; x 2 = 0 ; x 3 = 1   ; x 4 = 2   x 5 = 3 ; x 6 = 4

Portanto:

∫ - 2 4 f x d x ≈ R 6 = f - 1 + f 0 + f 1 + f 2 + f 3 + f 4 ⋅ 1  

Ou seja:

∫ - 2 4 f x d x ≈ R 6 = - 1,5 + 0 + 1,5 + 0,5 - 1 + 0,5 ⋅ 1 =   0

Logo:

∫ - 2 4 f x d x ≈ 0

Resposta

∫ - 2 4 f x d x ≈ 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita a parte (a) usando extremos esquerdos.
Repita a parte (a) usando extremos esquerdos.
Estime a área sob o gráfico de f x = 1 / x de x = 1 até x = 5 usando quatro retângulos aproximantes e extremos direitos. Esboce o gráfico e os retângulos. Sua estimativa é uma subestimativa ou uma sup
Estime a área sob o gráfico de f x = 25 - x 2 de x = 0 até x = 5 usando quatro retângulos aproximantes e extremos direitos. Esboce o gráfico e os retângulos. Sua estimativa é uma subestimativa ou supe
A velocidade de um corredor aumenta regularmente durante os três primeiros segundos de uma corrida. Sua velocidade na metade do segundo intervalo é dada em uma tabela. Ache as estimativas superior e i