Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 27
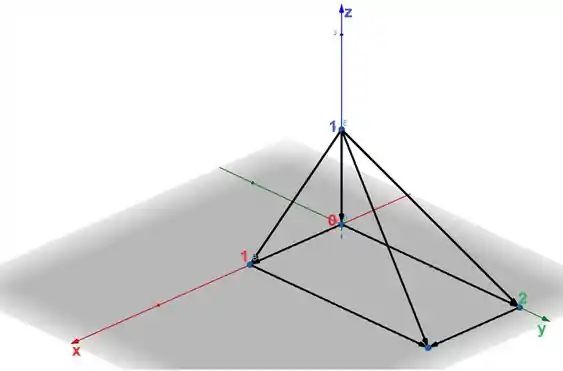
Esboce o sólido cujo volume é dado pela integral iterada.
Passo 1
Faaaaaala turma, tudo bem?
Nosso objetivo é esboçar o solido cujo volume é dado pela seguinte integral iterada:
Vamos pensa juntos!
Temos uma integral de volume do tipo
Onde,
E nossa região , pelas variações:
A partir dessa região que vamos esboçar o sólido.
Observe no eixo , o sólido está variando entre dois planos. São eles:
Já no eixo , o sólido está variando entre os planos:
Sabendo disso, a ideia é esboçar no tridimensional esses planos. Utilize o Geogebra, ele vai facilitar a compreensão dos planos no tridimensional.
Borá fazer isso!!!
Passo 2
Vamos focar primeiro nos planos em .
Sabemos que o solido está entre os dois planos:
Vamos ver como fica esse esboço com o Geogebra. Logo temos:
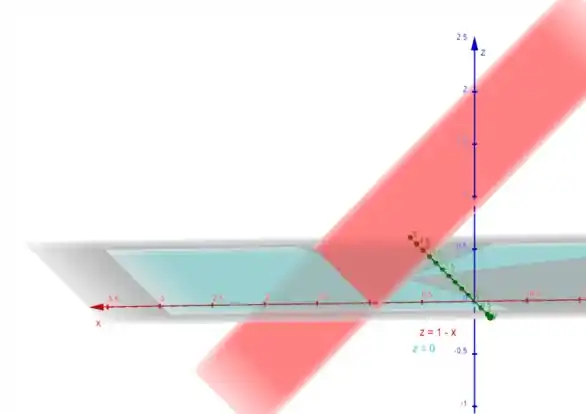
O plano inclinado em vermelho é o plano . Já o plano em azul que está no plano , é o plano .
Agora vamos avaliar os planos em .
Temos que o sólido está entre os seguintes planos:
Novamente utilizando o Geogebra, vamos ter:
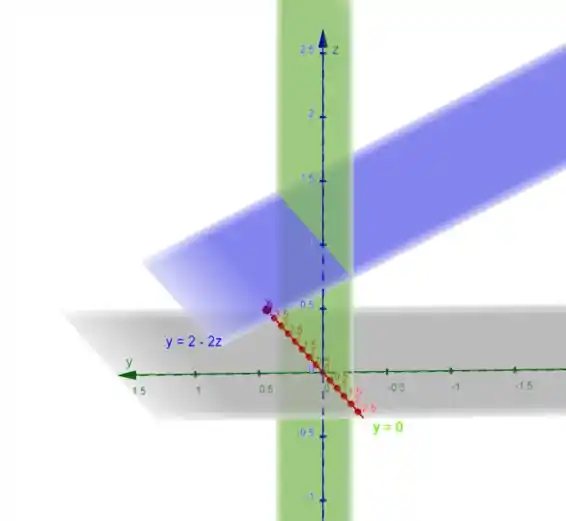
O plano inclinado em roxo é o plano . Já o plano em verde que está no plano , é o plano .
Passo 3
Agora vamos unir os quatros sólidos que encontramos.
Fazendo isso com o auxílio do Geogebra vamos ter o seguinte sólido:
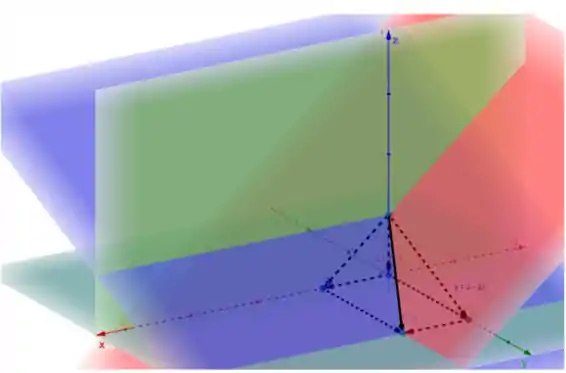
Nesta imagem temos os quatros planos, e foque na figura formado pelas linhas em preto. Essa figura é união dos pontos de encontro dos planos, e também onde eles cortam os eixos.
Elas surgem dessas limitações imposta no enunciado:
Lembra que ele falou no enunciado que o intervalo de varia de:
E também sabemos que ele é limitado pelos planos:
Portanto o sólido de nosso interesse é exatamente o sólido formado pelas linhas pretas. Olhe essa figura:
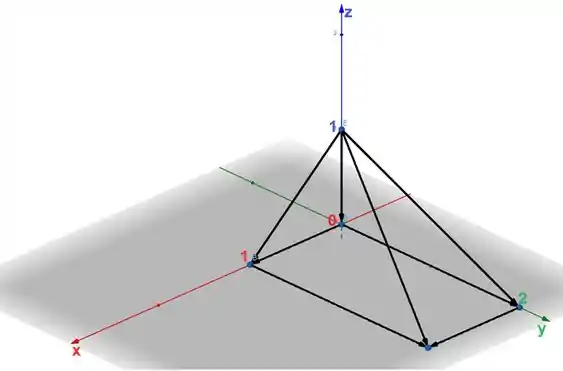
Resposta
