Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.2 - Ex. 39
Um barqueiro quer atravessar um canal que fica a 3 km de largura e quer atracar em um ponto 2 km acima do seu ponto de partida. A corrente flui no canal a 3,5 km/h e a velocidade do seu barco é 13 km/h
- Em que direção ele deve fugir?
- Quanto tempo a viagem vai demorar?
Passo 1
Vetorialmente, temos o seguinte problema:
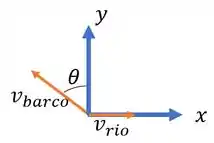
O barco quer fazer uma trajetória tal que ele percorra 3 km na direção do eixo e -2 km na direção do eixo .
O barco está sujeito a correnteza do rio na direção do eixo , e também está sujeito a sua própria velocidade, a qual possui componentes tanto na direção do eixo quando na direção do eixo .
Para resolvermos ambos os itens, torna-se necessário obter a equação da posição do barco. Somente a partir disto, vamos conseguir obter a direção de fuga e o tempo de travessia.
Passo 2
Vamos começar obtendo a equação vetorial da velocidade. Desta forma, temos:
Integrando a função e aplicando a condição de contorno que, em , o barco partiu da origem, temos a seguinte função posição:
Portanto, queremos descobrir os valores de e tais que:
Logo,
Resolvendo esta equação, obtemos que
Já para descobrirmos o tempo, basta substituir o valor de em qualquer uma das equações. Desta forma, temos:
Resposta
- , ângulo formado entre a direção do barco e a largura do rio.
- .