Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.3 - Ex. 42

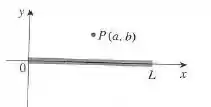
Uma barra carregada de comprimento L produz um campo elétrico no ponto P a , b dado por

E P = ∫ - a L - a λ b 4 π ϵ 0 x 2 + b 2 3 2 d x

Em que λ é a densidade de carga por unidade de comprimento da barra e ϵ 0 , a permissividade do vácuo. Calcule a integral para determinar a expressão para o campo elétrico E P

Passo 1

Primeiramente, não se desespera, calma e vamos trabalhar.

Pra facilitar, vamos dizer que

k = λ 4 π ϵ 0

Então

E P = ∫ - a L - a λ b 4 π ϵ 0 x 2 + b 2 3 2 d x = ∫ - a L - a k b x 2 + b 2 3 2 d x = k ∫ - a L - a b x 2 + b 2 3 2 d x

Agora, vamos fazer uma substituição trigonométrica, vamos dizer que

x = b tan ⁡ θ

Diferencidando, temos que

d x = b sec 2 ⁡ θ d θ

Não vamos calcular os novos limites de integração, depois vamos voltar com a variável x e usar os limites que estão mostrados para a integral calculada em x . Então, substituindo

k ∫ - a L - a b x 2 + b 2 3 2 d x = k ∫ i * i * * b b 2 tan 2 ⁡ θ + b 2 3 2 b sec 2 ⁡ θ d θ = k ∫ i * i * * b 2 b 2 tan 2 ⁡ θ + 1 3 2 sec 2 ⁡ θ d θ = k ∫ i * i * * b 2 b 2 sec 2 ⁡ θ 3 2 sec 2 ⁡ θ d θ = k ∫ i * i * * b 2 b 3 sec 3 ⁡ θ sec 2 ⁡ θ d θ = k b ∫ i * i * * 1 sec ⁡ θ d θ = k b ∫ i * i * * cos ⁡ θ d θ = k b sin ⁡ θ i * i * *

Passo 2

Agora, precisamos encontra sin ⁡ θ em função de x , pra isso, dissemos no início

x = b tan ⁡ θ

Podemos ver que

x 2 + b 2 = b sec ⁡ θ

Então

sec ⁡ θ = 1 cos ⁡ θ = x 2 + b 2 b

Logo

cos ⁡ θ = b x 2 + b 2

Com essas informações, podemos concluir que

tan ⁡ θ = sin ⁡ θ cos ⁡ θ = x b

Então

sin ⁡ θ = x b ⋅ b x 2 + b 2 = x x 2 + b 2

Passo 3

Agora, vamos substituir a expressão de sin ⁡ θ no resultado obtido, então

k b sin ⁡ θ i * i * * = k b x x 2 + b 2 - a L - a = k b L - a L - a 2 + b 2 + a a 2 + b 2 = k = λ 4 π ϵ 0 b L - a L - a 2 + b 2 + a a 2 + b 2

Resposta

E P = λ 4 π ϵ 0 b L - a L - a 2 + b 2 + a a 2 + b 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 35-48, utilize uma substituição apropriada e, em seguida, uma substituição trigonométrica para calcular as integrais. ∫ 1 / 12 1 / 4 2 d t t + 4 t t
Nos Exercícios 35-48, utilize uma substituição apropriada e, em seguida, uma substituição trigonométrica para calcular as integrais. ∫ x d x 1 + x 4
Nos Exercícios 15-34, use qualquer método para calcular as integrais. A maioria exigirá substituições trigonométricas, mas algumas podem ser calculadas por outros métodos. ∫ 1 - r 2 5 / 2 r 8 d r
Nos Exercícios 35-48, utilize uma substituição apropriada e, em seguida, uma substituição trigonométrica para calcular as integrais. ∫ ln ⁡ ( 3 / 4 ) ln ⁡ ( 4 / 3 ) e t d t 1 + e 2 t 3 / 2
Nos Exercícios 35-48, utilize uma substituição apropriada e, em seguida, uma substituição trigonométrica para calcular as integrais. ∫ 0 ln ⁡ 4 e t d t e 2 t + 9