Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 63
A beirada inferior de um quadro de pés de altura em exposição está pés acima do nível dos olhos de um observador. Supondo que a melhor visão é obtida quando é máximo o ângulo subentendido pelo quadro no olho do observador, a qual distância do quadro este deveria ficar?
Passo 1
Então pessoal, a fim de facilitar nossa visualização sobre o problema vamos esboçar essa situação aí, se liga:
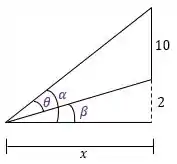
Aqui vale ressaltar duas coisas: o observador está na origem da figura e, claro, o desenho não está em escala. No entanto, são informações adicionais apenas, ok? Show! O que queremos aqui é encontrar uma expressão para em função de , galera! Pelo desenho temos que:
Então temos que determinar expressões para e antes de iniciarmos os cálculos com , beleza? Então bora que bora!
Passo 2
Para o triângulo retângulo envolvendo temos o seguinte:
Logo:
E para o triângulo envolvendo temos o seguinte:
Logo:
Sendo assim, nossa expressão será:
Perfeito!
Passo 3
Como estamos interessados em maximizar o ângulo em questão, então vamos utilizar os conceitos que aprendemos em cálculo! Derivando nossa função:
Simplificando:
Igualando a zero:
A única forma disso dar zero é se:
Como nosso intervalo é (pela figura do passo 1), então nosso ponto crítico é:
E esse é o ponto em que maximiza nosso ângulo , galera! 😊
Resposta
Ponto: .