Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.1 (exercícios de compreensão) - Ex. 4
4. A tabela a seguir dá a previsão de cinco dias de temperaturas máximas e mínimasem graus Celsius (°C).
(a) Suponha que x e y denotem, respectivamente,as previsões de temperaturas máxima e mínima paracada um doscinco dias. Será y uma função de x? Sefor, dê o domínio e a imagem dessa função.
(b) Suponha que x e y denotem, respectivamente,as previsões de temperaturas mínima e máxima paracada um doscinco dias. Será y uma função de x? Se for, dê o domínio e a imagem dessafunção
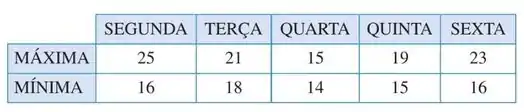
Passo 1
Aqui ele diz que denota previsão de temperatura máxima e de temperatura mínima
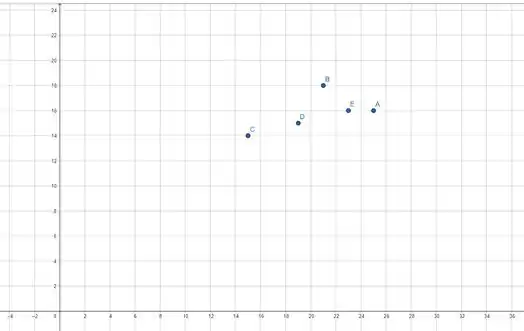
Se uma variável depende de uma variável de tal modo que cada valor de determina exatamente um valor de , então dizemos que é uma função de
Ou seja, para cada valor de só podemos ter um valor de
Show, para cada valor de só temos um valor de , então nosso domínio é
Passo 2
Já na letra temos isso aqui
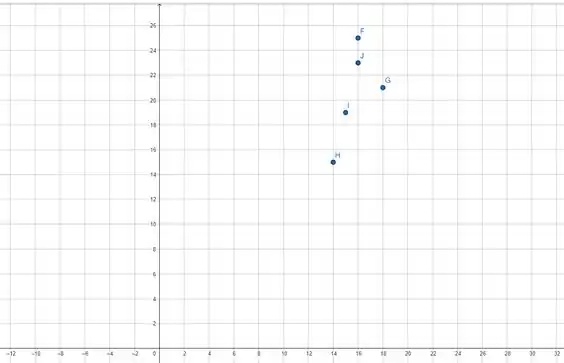
Agora, podemos ver que para temos dois valores de
Então não é função de
Resposta
Ei, a resposta está no passo a passo :)