Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.2 - Ex. 20
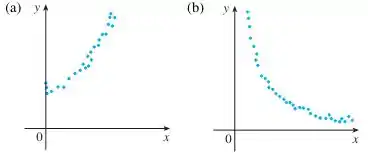
Para cada diagrama de dispersão, decida qual tipo de função você escolheria como um modelo para os dados. Explique sua escolha.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá dois diagramas de dispersão:
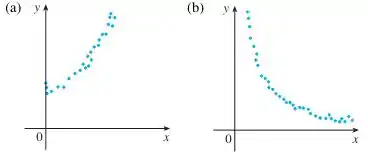
Queremos dizer o tipo de função que descreve os diagramas de dispersão dados.
Para isso, temos que imaginar uma curva que se assemelhe com a distribuição de pontos apresentadas e verificar a função que se parece.
Quer saber como?? Bora junto!!!
Passo 2
Vamos tentar traçar uma curva parecida com o diagrama da letra (a):
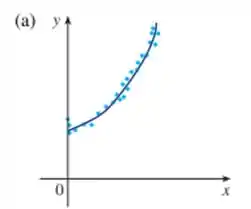
Podemos perceber uma função que cresce exponencialmente a partir de um ponto.
Então, uma função exponencial crescente ajusta bem os pontos. Essa função é dada da seguinte forma:
Onde:
- é a variável dependente;
- é a variável independente;
- é o termo de interceptação no eixo ;
- é o coeficiente que afeta a amplitude da curva exponencial;
- é o coeficiente de taxa de crescimento ou decaimento;
- é o número de Euler.
- é a variável dependente;
- é a variável independente;
- é o termo de interceptação no eixo (a amplitude da função).
Passo 3
Já no item (b), de forma análoga, temos:
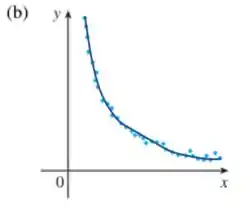
Podemos perceber que à medida que se aproxima de zero tende ao infinito e à medida que tende a infinito se aproxima de zero.
Dessa forma precisamos de uma função onde e sejam inversamente proporcionais.
Assim, uma hipérbole descrescente do tipo parece ajustar bem os pontos:
Onde: