Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.2 - Ex. 19
Para cada diagrama de dispersão, decida qual tipo de função você escolheria como um modelo para os dados. Explique sua escolha
Passo 1
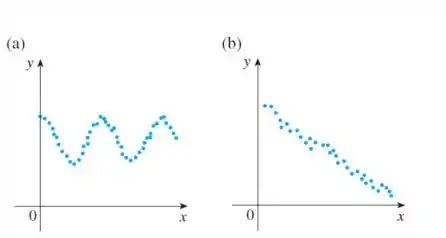
E aí, tudo bem?! Esse problema nos dá dois gráficos de dispersão:
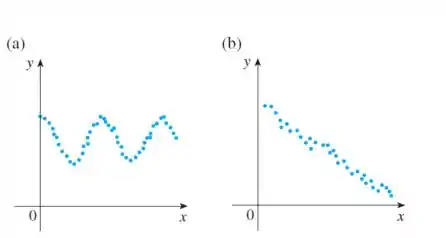
A gente precisa analisar os seus formatos e deduzir o tipo de função que pode representar bem esses dados!
Aqui não tem muito mistério, vamos pensar em qual tipo de curva se encaixa melhor com cada diagrama de dispersão e escrever uma fórmula geral pra ela, afinal aqui a gente não tem nenhum tipo de escala, logo não daria pra definir o modelo preciso! Bora lá?
Passo 2
Vamos começar com a letra (a):
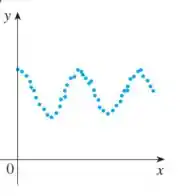
O que você vê nesse diagrama?!
Eu vejo vários altos e baixos e me parece com uma função periódica, concorda?!
Podemos ver também que ela começa pelo seu valor máximo, assim como a função:
Só que ela nunca corta o eixo , então podemos concluir que tem um elemento somando nessa função:
Não podemos afirmar que o cosseno ta sozinho, pois não temos escala, então podemos acrescentar:
Aqui a gente sabe com certeza que , já o e o só tão aí porque a gente não tem escala, assim eles podem ser por exemplo!
Passo 3
Agora a letra b:
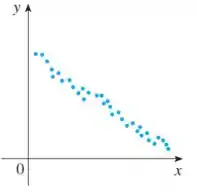
Essa é bem mais familiar! Vemos que os dados decrescem a medida que cresce. Eles tem um comportamento linear decrescente, podemos escrever que:
Onde .
Prontinho!