Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.6 - Ex. 13
Cada um dos Exercícios 11-16 apresenta o gráfico de uma função . Copie o gráfico e sobreponha-o à reta . Em seguida, utilize a simetria com relação à reta para adicionar o gráfico de ao seu esquema (não é necessário determinar uma fórmula para ). Identifique o domínio e a imagem de .
Passo 1
Então galera, assim como discutido na seção 6 do George, temos que para resolver os exercícios do 11-16 só precisamos lembrar de dois conceitinhos básicos sobre funções inversas, ok?
O primeiro conceito nos diz que o gráfico da função inversa é simétrico à reta , ou seja, para encontrarmos o gráfico da função sem utilizar de cálculos, basta refletirmos o gráfico da que nos é dada em torno da reta , beleza?
O segundo conceito nos diz o seguinte:
Seja e o domínio e a imagem de uma função , respectivamente, isso implica que o domínio da passará a ser e a imagem da passará a ser . Em outras palavras, as coisas só se invertem! Sabendo disso, já conseguimos resolver as questões. Bora lá!
Passo 2
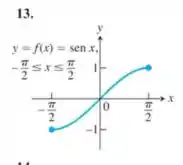
A função que nos foi dada é:
Se pegarmos o gráfico dessa função e refletirmos em torno de , teremos:
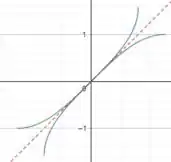
No qual é a função pontilhada; é a função verde e é a função azul.
Passo 3
Agora que temos o gráfico das funções, vamos utilizar o segundo conceito comentado no passo 1 para descobrimos o domínio e a imagem de , tranquilo?
Domínio de
Imagem de
Domínio de
Imagem de
Resposta
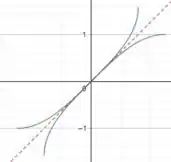
Domínio de
Imagem de