Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.3 - Ex. 53

Para os Exercícios 51-54 encontre o ângulo θ , onde 0 ≤ θ ≤ 2 π .

53. sen ⁡ 2 θ - cos ⁡ θ = 0

Passo 1

Precisamos simplificar a equação. A gente pode utilizar a fórmula do arco duplo no primeiro termo:

sen ⁡ 2 θ = 2 sen ⁡ θ cos ⁡ θ

A equação fica:

2 sen ⁡ θ cos ⁡ θ - cos ⁡ θ = 0

Colocando cos ⁡ θ em evidência vamos ter:

cos ⁡ θ ⋅ 2 sen ⁡ θ - 1 = 0

Para esse produto ser igual a zero só existem duas possibilidades: ou cos ⁡ θ = 0 , ou 2 sen ⁡ θ - 1 = 0 . Então vamos achar quais ângulos fazem com que uma das duas opções seja verdadeira.

Passo 2

Para cos ⁡ θ = 0

Existem duas possibilidades, π 2   e 3 π 2 :

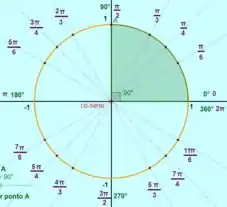
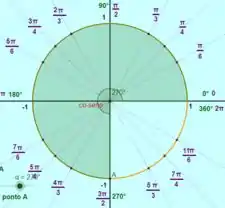
Para 2 sen ⁡ θ - 1 = 0

2 sen ⁡ θ = 1

sen ⁡ θ = 1 2

Também existem duas possibilidades para esse caso, π 6   e 5 π 6 :

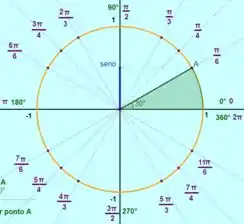
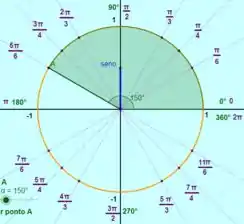
Logo qualquer um desses quatro ângulos vai fazer satisfazer a equação

Resposta

θ = π 2 ,     θ = 3 π 2 ,     θ = π 6 ,     θ = 5 π 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça os gráficos das funções nos Exercícios 13-22. Qual o período de cada função? - c o s( 2 π x )
Faça os gráficos das funções nos Exercícios 13-22. Qual o período de cada função? - s e n( π x 3 )
Faça os gráficos das funções nos Exercícios 13-22. Qual o período de cada função? s e n( x +π 6 )
Copie e complete a tabela a seguir com valores de funções. Se a função não for definida para um dado ângulo, preencha com "ND". Não use calculadora ou tabelas.
Copie e complete a tabela a seguir com valores de funções. Se a função não for definida para um dado ângulo, preencha com "ND". Não use calculadora ou tabelas.