Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 66

Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar a forma geral do gráfico de f.

66-

y ' = x 2 - 2 x x - 5 2

Passo 1

Fazendo y ' = 0 com o objetivo de encontrarmos os pontos críticos da função temos:

Ou:

x 2 - 2 x = 0

Ou:

x - 5 = 0

Na primeira equação temos: x = 0 e x = 2 como pontos críticos e na segunda equação temos somente x = 5

Logo temos como pontos críticos:

x = 0 ;         x = 2         ; x = 5

Passo 2

Derivando a equação a fim de encontrarmos nosso y ' ' temos:

y ' ' = x 2 - 2 x ' x - 5 2 + x 2 - 2 x ( x - 5 2 ) '

y ' ' = 2 x - 2 x - 5 2 + 2 ( x 2 - 2 x ) ( x - 5 )

Isolando x - 5 :

y ' ' = x - 5 [ 2 x - 2 x - 5 + 2 x 2 - 2 x ]

Fazendo o produto notável e depois isolando o número 2 temos:

y ' ' = 2 ( x - 5 ) ( 2 x 2 - 8 x + 5 )

Passo 3

Agora dessa segunda derivada tiramos nossos pontos de máximo e mínimo e pontos de inflexão:

Para x = 0 :

y ' ' ( 0 ) = 2 0 - 5 2 × 0 2 - 8 × 0 + 5 = - 50 → n e g a t i v o

Logo x = 0 representa um ponto de máximo local.

Para x = 2 :

y ' ' 2 = 2 2 - 5 2 × 2 2 - 8 × 2 + 5 = 2 × - 3 × - 3 → p o s i t i v o

Logo x = 2 representa um ponto de mínimo local

Para x = 5 :

y ' ' 5 = 2 5 - 5 2 × 5 2 - 8 × 5 + 5 → 0

Logo não podemos afirmar nada sobre x = 5 , ele pode representar um ponto de inflexão, máximo ou mínimo local ou uma singularidade. Somente iremos saber ao analisar seus intervalos:

Pontos de inflexão:

y ' ' = 0

2 x - 5 2 x 2 - 8 x + 5 = 0

Para essa expressão ser zero ou:

x - 5 = 0 → x = 5

Como já vimos

Ou:

2 x 2 - 8 x + 5 = 0

Que resolvendo por Bhaskara encontramos como pontos de inflexão:

x = 2 ± 6 2

Ou aproximadamente:

x = 0.775 ;           x = 3.22

Passo 4

Organizando nossos intervalos temos:

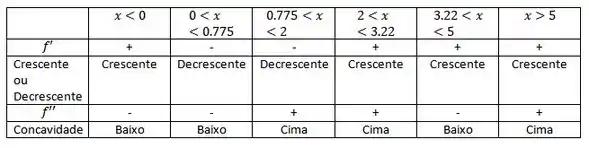
Valores de Teste: -1 , 0.5, 1, 3, 4, 6

Resposta

y ' ' = 2 ( x - 5 ) ( 2 x 2 - 8 x + 5 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

55-60. Usando a regra de L’Hôpital (Seção 3.6), podemos conferir que: lim x → + ∞ ⁡ ln ⁡ x x r = 0 ,lim x → + ∞ ⁡ x r ln ⁡ x = + ∞ ,lim x → 0 + ⁡ x r ln ⁡ x = 0 Com qualquer número real positivo r . N
39-44. Obtenha um gráfico da função e identifique a localização de todos os pontos de extremos relativos e de inflexão. Confira seu trabalho com um recurso gráfico.44. tan ⁡ x ,0 ≤ xπ 2
45-54. Usando a regra de L’Hôspital (Seção 3.6), podemos conferir que: lim x → + ∞ ⁡ e x x = + ∞ ,lim x → + ∞ ⁡ x e x = 0 ,lim x → - ∞ ⁡ x e x = 0 Nestes exercícios:a) use esses limites, se necessário
45-54. Usando a regra de L’Hôspital (Seção 3.6), podemos conferir que: lim x → + ∞ ⁡ e x x = + ∞ ,lim x → + ∞ ⁡ x e x = 0 ,lim x → - ∞ ⁡ x e x = 0 Nestes exercícios:a) use esses limites, se necessário
45-54. Usando a regra de L’Hôspital (Seção 3.6), podemos conferir que: lim x → + ∞ ⁡ e x x = + ∞ ,lim x → + ∞ ⁡ x e x = 0 ,lim x → - ∞ ⁡ x e x = 0 Nestes exercícios:a) use esses limites, se necessário