Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 74

Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar a forma geral do gráfico de f.

74-

y ' = sin ⁡ t

0 ≤ t ≤ 2 π

Passo 1

Fazendo y ' = 0 para encontrarmos os pontos críticos da função nós temos:

sin ⁡ t = 0

No intervalo que vai de 0 a 2 π onde incluímos esses pontos o sin ⁡ t irá ser 0 nesses pontos:

t = 0 ;   t = π ;     t = 2 π

Passo 2

Fazendo agora a segunda derivada dessa função para saber o comportamento dos pontos que encontramos e seus pontos de inflexão:

y ' ' = cos ⁡ t

Passo 3

Agora testando os pontos que encontramos no passo 1 temos:

Para t = 0

y ' ' 0 = cos ⁡ 0 = 1 → p o s i t i v o

Logo em t = 0 temos um ponto de mínimo local.

Para t = π

y ' ' π = cos ⁡ π = - 1 → n e g a t i v o

Logo em t = π temos um ponto de máximo local.

Para t = 2 π

y ' ' 2 π = c o s   2 π = 1 → p o s i t i v o

Logo em t = 2 π temos também um ponto de mínimo local.

Agora os pontos de inflexão:

cos ⁡ t = 0

No intervalo de 0 a 2 π temos que o cosseno é igual a 0 nos pontos:

t = π 2 ;         t = 3 π 2

Passo 4

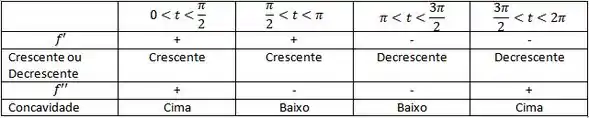
Ponto de teste em radianos: 1, 2, 4, 5

Resposta

y ' ' = cos ⁡ t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = e x
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,0 ≤ x2
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,0x ≤ 2
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = 1 - x s e0 ≤ x2 2 x - 4 s e2 ≤ x ≤ 3
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f t = 1 t,01t