Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 6.2 - Ex. 42

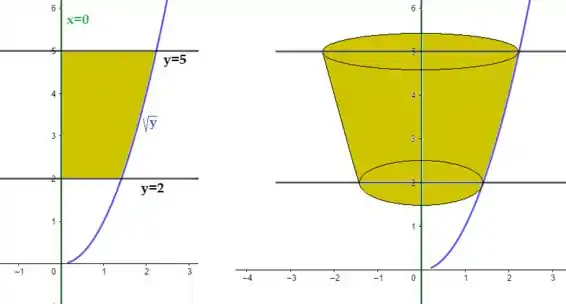
Cada integral representa o volume de um sólido. Descreva o sólido.

Passo 1

Olá, meu amigo. Yuri aqui e estarei te ajudando nessa atividade.

Aqui iremos realizar um caminho inverso do habitual, costumam nos pedir para calcularmos o volume do solido, agora iremos aqui encontrar qual o solido dado que temos a equação do seu volume.

Muito bem galera, antes de começar vamos lembrar como se calcula o volume de um sólido de rotação:

Então qual a área da figura que irá rotacionar?

Para saber vamos reorganizar o volume que o problema nos deu:

Então a área é dada por:

Passo 2

Vamos com calma! Essa área nos dá mais uma informação. Quando calculamos a área nós subtraímos a função do seu eixo de rotação, ao quadrado:

Podemos concluir então que:

Concluímos então que o sólido é originado pela rotação da função sobre o eixo y.

Então, a região delimitada aqui é:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a região mostrada na figura for girada em torno do eixo x para formar um sólido, use a Regra do Ponto Médio, comn = 4 , para estimar o volume do sólido.Estime o volume se a região for girada em tor

Cada integral representa o volume de um sólido. Descreva o sólido. π ∫ 0 π / 2 [ 1 + cos ⁡ x 2 - 1 ² ] . d x ²

Encontre o volume do sólido S descrito. Um cone circular reto com altura h e raio da base r .

Encontre o volume do sólido S descrito. Um tronco de cone circular reto de altura h , raio da base inferior R e raio da base superior r .

Um modelo para a forma do ovo de um pássaro é obtido girando, em torno do eixo x , a região sob o gráfico de f x = a x 3 + b x 2 + c x + d ) 1 - x 2 Use um SCA para encontrar o volume deste ovo.Para u