Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 48

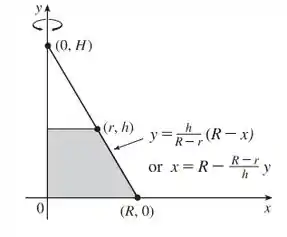
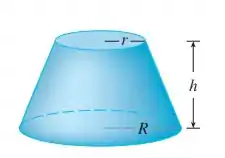
Encontre o volume do sólido S descrito. Um tronco de cone circular reto de altura h , raio da base inferior R e raio da base superior r .

Passo 1

Para formar essa figura nós temos um triângulo retângulo girando em torno do eixo y , com a parte superior sendo recortada. Podemos formar a seguinte figura para análise:

Passo 2

V = π ∫ 0 h R - R - r h y 2 d y = π ∫ 0 h R 2 - 2 R R - R h y + R - r h 2 y 2 d y =

π R 2 y - R R - r h y 2 + 1 3 R - r h 2 y 3 0 h = π R 2 y - R R - r h + 1 3 R - r 2 h =

1 3 π h 3 R r + R 2 - 2 R r + r 2 = 1 3 π h ( R 2 + R r + r 2 )

Resposta

V = 1 3 π h ( R 2 + R r + r 2 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada. R 3e mt o r n od eO C
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada. R 2e mt o r n od eO C
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada. R 3e mt o r n od eB C
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada. R 3e mt o r n od eA B
Cada integral representa o volume de um sólido. Descreva o sólido. π ∫ 0 1 y 4 - y 8 d y