Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 47
Encontre o volume do sólido descrito. Um cone circular reto com altura e raio da base .
Passo 1
Opa! Bora resolver esse problema! Queremos o volume de um cone circular reto com altura e raio da base .
Como podemos fazer isso?!
Podemos rotacional a região delimitada pelas retas:
Em torno do eixo . Se liga no gráfico dessa região:
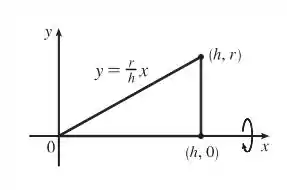
Com a rotação formaremos um cone com as dimensões que o enunciado pede!
Passo 2
Para calcular o volume temos:
Essa área é dada por:
Substituindo na fórmula do volume:
Prontinho!
Resposta
Exercícios de Livros Relacionados
Escreva, mas não calcule, uma integral para o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno da reta especificada. y = x - 2 4 ,8 x - y = 16 ; e mt o r n od oe i x
Escreva, mas não calcule, uma integral para o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno da reta especificada. y = c o sx ,y = 2 - cos x ,0 ≤ x ≤ 2 π ; e mt
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada. R 3e mt o r n od eO A
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada. R 2e mt o r n od eB C
Escreva, mas não calcule, uma integral para o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno da reta especificada. y = 0 ,y = s e nx ,0 ≤ x ≤ π ; e mt o r n od ey