Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 45

  1. Se a região mostrada na figura for girada em torno do eixo x para formar um sólido, use a Regra do Ponto Médio, com   n = 4 , para estimar o volume do sólido.

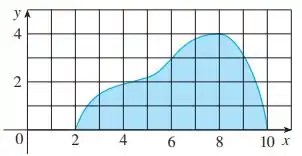
  2. Estime o volume se a região for girada em torno do eixo y . Novamente use a regra do ponto médio com n = 4 .

Passo 1

  1. V = ∫ 2 10 π [ f x ] ² d x

    2. A variação de x é:

    ∆ x = 10 - 2 4 = 2

    Os pontos extremos são 2 ,   4 ,   6 ,   8 e 10 , e os pontos médios, 3 ,   5 ,   7 e 9 .

    V ≈ 2 π [ 1.5 2 + 2.2 2 + 3.8 2 + 3.1 2 ] ≈ 196 u n i d a d e s ³

    Passo 2

  2. V = ∫ 0 4 π r a i o   e x t e r n o 2 - r a i o   i n t e r n o 2 d y

V ≈ π 4 - 0 4 9.9 2 - 2.2 2 + 9.7 2 - 3 2 + 9.3 2 - 5.6 2 + 8.7 2 - 6.5 ≈ 838 u n i d a d e s ³

Resposta

  1. V ≈ 196 u n i d a d e s ³
  2. V ≈ 838 u n i d a d e s ³
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. y = x 3 ; y = x ; x ≥ 0 ; Em torno do eixo x .
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = x 2 / 3 ,x = 1 ,y =
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y 2 = x ,x = 2 y ;e mt o
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = 1 x ,y = 0 , x = 1 ,
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = x ,y = x ;e mt o r n