Para cada um dos números e , diga se a função cujo gráfico é dado tem um máximo ou mínimo absoluto, um máximo ou mínimo local, ou nem máximo, nem mínimo.
Passo 1
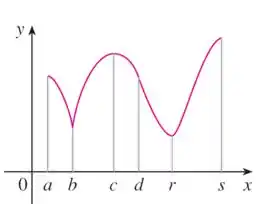
Nessa questãozinha temos o seguinte gráfico:
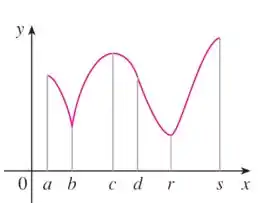
Aqui a gente tem diferentes pontos e . Temos que classifica-los em locais ou globais!
Lembrando que um mínimo local é um ponto tal que para todo em uma vizinhaça de , enquanto que um mínimo absoluto (ou global) é um ponto tal que para todo no domínio da função.
De uma forma mais simples, também podemos definir esses pontos assim:
- Máximo absoluto: é o ponto mais alto de todo o gráfico.
- Mínimo absoluto: é o ponto mais baixo de todo o gráfico.
- Máximos e mínimos locais: são picos ou vales em regiões próximas, mas não necessariamente os mais extremos.
- Nem máximo nem mínimo: ocorre quando a função não atinge pico/vale, por exemplo, em inflexões ou nas extremidades sem ponto de virada.
Passo 2
O ponto está no início da curva e não é um ponto alto nem baixo em relação aos arredores pois a função só começa a descer.
No ponto vemos um vale, onde a função atinge um ponto mínimo ali e depois sobe. Assim, trata-se de um mínimo local (não é global);
O ponto mostra um pico, a função atinge um ponto alto local e depois desce. Assim, trata-se de um máximo local (não absoluto);
O ponto é um ponto de inflexão (a concavidade muda, mas não é um pico ou vale). Assim, não é nem máximo, nem mínimo;
Já no ponto a função atinge o ponto mais baixo de todo o gráfico. Assim, trata-se de um mínimo global.
Por fim, o ponto é máximo absoluto (é o ponto mais alto do gráfico).
Resposta
Máximo local: .
Mínimo local: .
Máximo global: .
Mínimo global: .
Nem máximo e nem mínimo: e .