A caneca mostrada na figura está sendo enchida com café a uma taxa constante (medida em volume por unidade de tempo). Esboce um gráfico da profundidade do café na caneca como uma função do tempo. Forneça uma explicação para o formato do gráfico em termos de concavidade. Qual o significado do ponto de inflexão?

Vamos pensar um pouquinho em relação as derivadas dessa função, a nossa função será:

Onde é a profundidade do café. O enunciado diz que:

Podemos dizer que:

Onde é a área transversal. Então:

Então:

Essa derivada vai ser sempre positiva, afinal se estamos enchendo uma caneca a profundidade de líquido irá sempre aumentar. Pra descobrir a concavidade precisaríamos de uma segunda derivada:

Teremos uma concavidade pra cima quando a derivada segunda for positiva e uma concavidade pra baixo quando ela for negativa.

Vamos voltar a analisar a imagem:

A área inferior é maior e vai diminuindo até chegar a um ponto mínimo, na metade da altura da caneca, nesse momento ela volta a aumentar até chegar ao tomo da caneca onde podemos supor que a área é igual a área de baixo.

Se a área esta diminuindo, então:

Portanto:

Temos aqui uma função crescente com concavidade pra cima. Quando a área aumenta temos:

Portanto:

Temos aqui uma curva com concavidade pra baixo.

No ponto de mínimo teremos:

Assim:

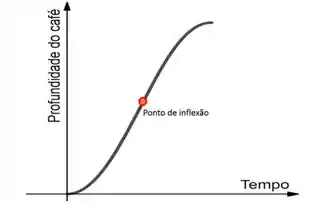
Esse vai ser nosso ponto de inflexão! Agora adicionando essas informações ao gráfico:

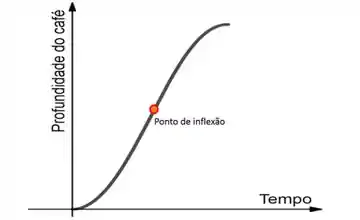
Prontinho!!