Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 4
Para cada um dos números e , diga se a função cujo gráfico é dado tem um máximo ou mínimo absoluto, um máximo ou mínimo local, ou nem máximo, nem mínimo.
Passo 1
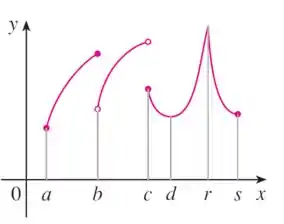
Opa, bora resolver esse problema! Temos o seguinte gráfico:
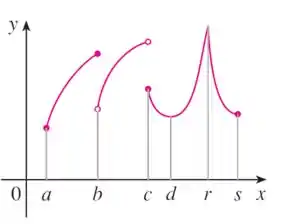
Aqui a gente tem diferentes pontos e . Temos que classifica-los em locais, globais ou nem máximo, nem mínimo!
Lembrando que um mínimo local é um ponto tal que para todo em uma vizinhaça de , enquanto que um mínimo absoluto (ou global) é um ponto tal que para todo no domínio da função.
Passo 2
O ponto é um ponto de mínimo global pois ele é o menor valor de todo o domínio da função!
O ponto é um máximo local, a gente sabe disso pois antes dele os valores são menores e depois dele os valores são menores também! Só fica antento a bolinha aberta e fechada, o ponto é aquele com a bolinha fechada!
O ponto não é um máximo nem um mínimo, pois a sua esquerda temos valores maiores e a direita menores!
O ponto é um mínimo local pois vemos uma diminuição em a sua esquerda e direita.
O ponto é um máximo local pois aumeta a sua direita e esquerda.
O ponto não é um máximo nem um mínimo, pois a sua esquerda temos valores maiores e a direita não temos nenhum valor!
Resposta
Máximo local: ; mínimo local: , e ; máximo global: ; mínimo global: a.