Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 (exercícios de compreensão) - Ex. 4
Em cada parte, determine o valor exato sem utilizar recursos computacionais
Passo 1
Fala povo, tudo certo? Ó só, pra gente matar essa questão bem rapidinho, vamos pensar o seguinte, como o enunciado fala tudo sobre arco de funções trigonométricas, se a gente lembrar por exemplo que:
Significa que é o arco cujo seno é , podemos reescrever todas as letras do enunciado:
Para:
Basicamente o que fizemos foi usar a função inversa das funções arco. Como as funções arco já são as inversas trigonométricas, voltamos pra elas. Bacana, não? Nosso objetivo então vai ser achar esses valores de ! Pra isso, vai nos ajudar muito olhar o círculo trigonométrico:
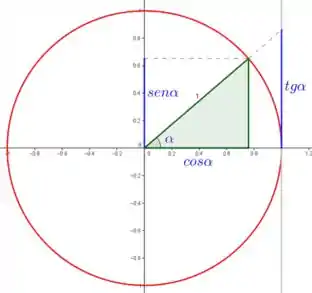
E essas relações pra ângulos clássicos dentro desse círculo:
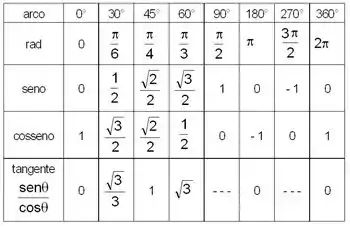
Uma coisa importante aqui de notar é que essa tabela só é importante de ter na cachola pros ângulos . Todos os outros a gente tira os resultados olhando o que acontece com o seno e o cosseno quando gira no sentido anti-horário. Por exemplo, com , olhando pelo círculo, vemos que o cosseno coincide com a hipotenusa do triângulo verde e o seno some.
Passo 2
Letra a)
Show galera, analisando e entendendo a tabelinha, a partir de agora é só uma questão de consultar ela pra responder. Olhando bem, vemos que:
Então a resposta da letra vai ser .
Letra b)
De novo, pela tabela, temos:
Portanto a resposta da letra vai ser .
Letra c)
Pela tabela:
Assim, a resposta da letra vai ser .
Letra d)
Pela tabela:
Assim, a resposta da letra vai ser .
Letra e)
Pra fechar, sendo:
Temos então que:
Pela tabela:
O que não é exatamente a mesma coisa, mas se analisarmos bem o círculo trigonométrico, vemos que esses dois ângulos tem o mesmo valor de cosseno em módulo:
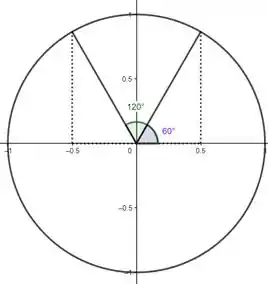
Sendo assim:
Então a resposta da letra vai ser .