Em cada parte, esboce uma curva contínua com as propriedades indicadas.
- , , com qualquer
- , , com , com
- , com e ,
Passo 1
- Com as propriedades da letra (a) podemos usar :
- Com as propriedades da letra (b) podemos usar :
- Com as propriedades da letra (c) podemos usar :
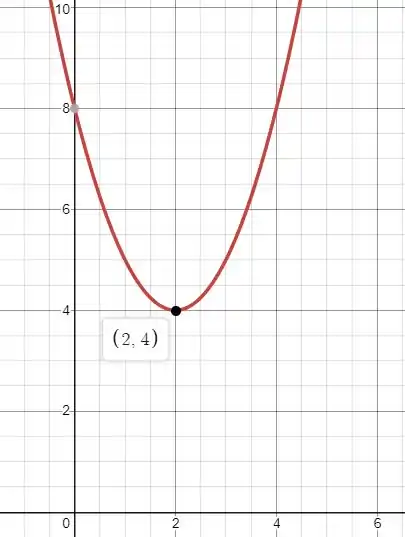
Vamos calcular , e e ver se obtemos o que é pedido:
Agora encontrando a primeira derivada:
Achando :
E achando :
Pronto, esboçamos a curva com as propriedades indicadas.
Passo 2
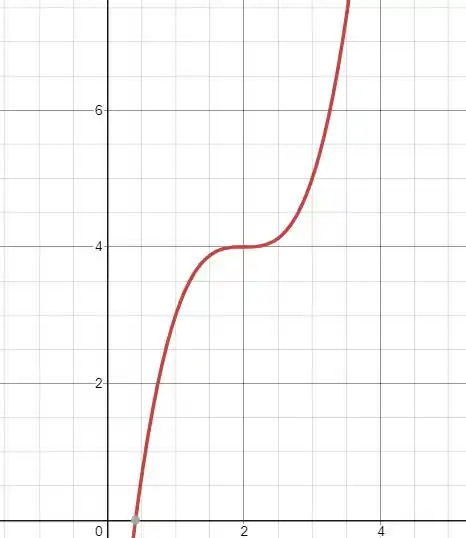
Vamos calcular , e e ver se obtemos o que é pedido:
Agora encontrando a primeira derivada:
Achando :
E achando :
Agora vamos ver onde é positiva e negativa igualando a zero e avaliando os sinais:
Analisando os sinais:
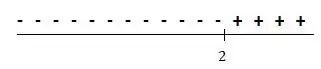
Temos então que com , com .
Pronto, esboçamos a curva com as propriedades indicadas.
Passo 3

Vamos calcular e e os limites para ver se obtemos o que é pedido:
Agora encontrando a primeira derivada:
Aqui temos que analisar melhora a função, porque uma função com módulo é da forma:
Então para temos:
E para temos:
E achando :
Para temos:
E para temos:
Analisando os sinais temos que para .
Agora vamos ver os limites:
Pronto, esboçamos a curva com as propriedades indicadas.
Resposta
Ei, a resposta está no passo a passo :)