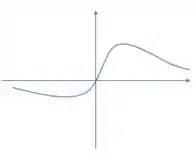
2. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas, onde .

b) tem exatamente dois extremos relativos em e quando e .

Então galera, aqui temos que pensar em uma função no qual o gráfico tenha apenas dois extremos relativos, além de quando e . Dessa forma, um gráfico possível seria:

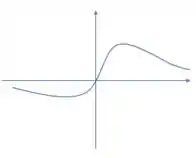
E aí como a questão só quer o esboço, não precisamos pensar em uma função para calcular os extremos e a concavidade a fim de provar nossa resposta.