Em cada parte, identifique o domínio e a imagem da função e, então, esboce o gráfico da função sem utilizar um recurso computacional.
Passo 1
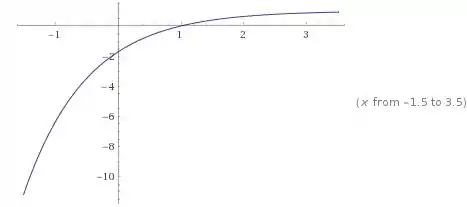
a)
A função que nós temos nesse item é a seguinte:
Que possui e .
Se nós esboçarmos o gráfico dessa função teremos a seguinte forma:
Passo 2
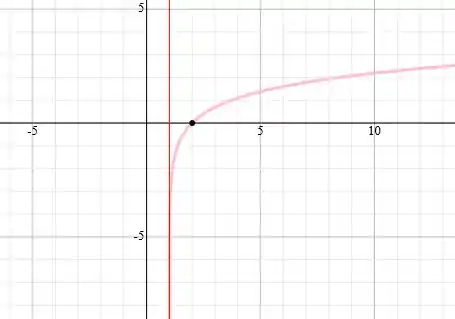
b)
A função que nós temos nesse item é a seguinte:
Que possui e .
Se nós esboçarmos o gráfico dessa função teremos a seguinte forma:
Resposta
Ei, a resposta está no passo a passo :)