Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.6 - Ex. 1
- Em cada parte, use uma integral definida para encontrar a área da região e verifique sua resposta usando uma fórmula apropriada de Geometria.
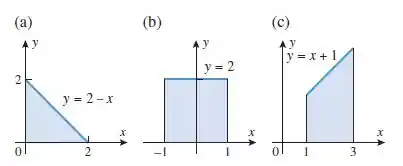
Passo 1
Vamos começar com a letra a), primeiro faremos pela integral definida.
Na letra a), estamos indo de até
Agora faremos pela área, o gráfico dessa função é um triângulo retângulo.
A área de um triângulo retângulo é dada por
O primeiro cateto vai de até , então mede
O segundo cateto vai de até , então mede
A área desse triângulo é então:
E como calculado tanto o cálculo da integral por antiderivada quanto pela área têm valores iguais.
Passo 2
Faremos a mesma coisa na letra b)
Na letra b), estamos indo de até
Agora faremos pela área, o gráfico dessa função é um retângulo.
A área de um retângulo é dada por
A base vai de até , então mede
O altura vai de até então mede
A área desse triângulo é então:
E como podemos perceber tanto o cálculo da integral por antiderivada quanto pela área têm valores iguais.
Passo 3
Igualmente para a letra c)
Na letra b), estamos indo de até
Agora faremos pela área, o gráfico dessa função é um trapézio.
A área de um trapézio é dada por
A base maior vai de até , então mede
A base menor vai de até , então mede
O altura vai de até então mede .
A área desse triângulo é então:
E como podemos perceber tanto o cálculo da integral por antiderivada quanto pela área têm valores iguais.
Resposta
a)
b)
c)