Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.9 - Ex. 5

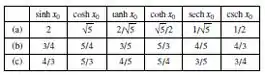
Em cada parte, um valor para uma das funções hiperbólicas é dado em um ponto não especificado x 0 . Use as identidades apropriadas para encontrar os valores exatos das cinco restantes funções hiperbólicas em x 0 .

(a) sinh ⁡ x 0 = 2 (b) cosh ⁡ x 0 = 5 4 (c) tanh ⁡ x 0 = 4 5

Passo 1

Para resolvermos esse problema, vamos precisar montar uma tabelinha, pois sabemos que as funções são dependentes uma das outras, assim, vamos começar calculando os itens.

Para o item (a),usamos a seguinte identidade:

cosh 2 ⁡ x 0 - sinh 2 ⁡ x 0 = 1

sinh 2 ⁡ x 0 = cosh 2 ⁡ x 0 - 1

sinh 2 ⁡ x 0 = 5 4 2 - 1 = 25 16 - 1 = 3 4

Para o item (b), usamos a mesma identidade:

cosh 2 ⁡ x 0 = 1 + sinh 2 ⁡ x 0

cosh 2 ⁡ x 0 = 1 + 2 2 = 5

E, por fim, para a tangente hiperbólica, usamos:

sech 2 ⁡ x 0 + tanh 2 ⁡ x 0 = 1

sech 2 ⁡ x 0 = 1 - tanh 2 ⁡ x 0

sech 2 ⁡ x 0 = 1 - 4 5 2 = 3 5

Passo 2

Para encontrarmos as outras funções, fazemos as combinações, ou ate mesmo da seguinte forma:

cosh ⁡ x 0 = 1 sech ⁡ x 0 = 5 3

Então, se sinh ⁡ x 0 cosh ⁡ x 0 = tanh ⁡ x 0 , podemos dizer que:

sinh ⁡ x 0 = 5 3 × 4 5 = 20 15 = 4 3

A partir desse modelo, montamos a seguinte tabela:

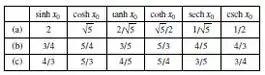
Prontinho!!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache a integral indefinida geral. 13 . ∫ sen ⁡ x + senh ⁡ x d x
Encontre dy/dx. y = sinh ( 4 x - 8 )
Encontre dy/dx. y = cosh ( x^4 )
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. As identidades do Teorema 6.9 . 2 podem ser obtidas das correspondentes identidades trigonométricas substituindo as funções
Prove que sinh ⁡ x é uma função ímpar de x , que cosh ⁡ x é uma função par de x e verifique que isso é consistente com os gráficos na Figura 6.9 . 1 .