Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 4.2 - Ex. 24

Em cada um dos problemas de 11 a 28 , encontre a solução geral da equação diferencial dada.

24. y ' ' ' + 5 y ' ' + 6 y ' + 2 y = 0

Passo 1

Para começar esse problema, podemos comparar a EDO que temos que resolver com a equação característica...

r 3 + 5 r 2 + 6 r + 2 = 0

Observe que - 1 é raiz dessa equação:

- 1 3 + 5 - 1 2 + 6 - 1 + 2 = 0   →

0 = 0

Então podemos fatorar usando Briot Rufini:

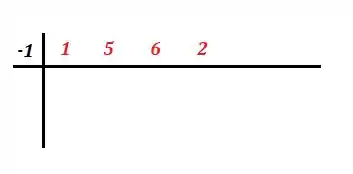
Onde os coeficientes em vermelho são os coeficientes da equação de grau 3 que queremos reduzir e 1 é o sua raiz. Então, aplicando o método...

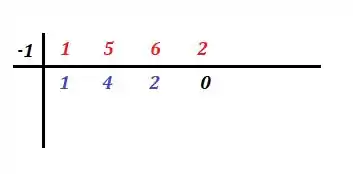
Então os coeficientes em azul são os coeficientes da equação reduzida:

r 2 + 4 r + 2 = 0

Então...

r 3 + 5 r 2 + 6 r + 2 = 0     →

r + 1 r 2 + 4 r + 2 = 0

A primeira raiz que tiramos daí é a raiz que já havíamos encontrado para aplicar...

r 1 = - 1

E para as demais:

r 2 + 4 r + 2 = 0

Usando Báskara...

r = - 4 ± 16 - 4 ⋅ 2 2     →

r = - 4 ± 8 2     →

r = - 4 ± 2 2 2     →

Logo, as outras duas raízes que tiramos daí é...

r 2 = - 2 + 2           e               r 3 = - 2 - 2

Passo 2

Beleza, então podemos montar a solução dessa EDO de acordo com os valores de r . Vamos nessa?

Vamos começar montando as soluções fundamentais para dada r :

  • Para r 1 = - 1 como ele é real...

    • y 1 = e r 1 t = e - t

  • Para r 2 = - 2 + 2 , por ser real e único...

    • y 2 = e r 2 t = e - 2 + 2 t

  • Para r 3 = - 2 - 2 , por ser real e único...

y 3 = e - 2 - 2 t

A solução geral então pode ser dada por...

y = c 1 y 1 + c 2 y 2 + c 3 y 3   →

y = c 1 e - t + c 2 e - 2 + 2 t + c 3 e - 2 - 2 t

Onde c ’s representam as constantes que dependem das condições iniciais!

Resposta

y = c 1 e - t + c 2 e - 2 + 2 t + c 3 e - 2 - 2 t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que a solução geral de y^(4) – y = 0 pode ser escrita como.Determine a solução que satisfaz as condições iniciais y(0) = 0, y′(0) = 0, y′′(0) = 1, y′′′(0) =1
Encontre a solução do problema de valor inicial dado e faça seu gráfico. Como a solução se comporta quando t → ∞? .
Nesse problema, esquematizamos um modo de mostrar que, se r1, . . . , rn forem reais e distintos, então e^r1t, . . . , e^rnt serão linearmente independentes em –∞ e mostrar que todas as constantes são
Encontre a solução do problema de valor inicial dado e faça seu gráfico. Como a solução se comporta quando t → ∞? .
Encontre a solução do problema de valor inicial dado e faça seu gráfico. Como a solução se comporta quando t → ∞? .