Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 5.4 - Ex. 15

Em cada um dos problemas de 13 a 16, encontre a solução do problema de valor inicial dado. Faça o gráfico da solução e descreva como ela se comporta quando x → 0

15.

x 2 y ″ -   3 x y ' +   4 y   =   0 ,

  y ( – 1 )   =   2 ,   y ' ( – 1 )   =   3  

Passo 1

Essa função tem o seguinte formato

P x y " + Q ( x ) y ' + R ( x ) y   =   0

E quando nosso enunciado nos fala sobre “ponto singular” ele está querendo dizer os pontos de x onde

P x = 0

Quaisquer outros pontos são chamados de ordinários. Beleza!!! O que faremos agora é supor que a solução do nosso problema é

y = x r

E com isso substituir na nossa equação

y ' = r x r - 1

y "   =   r ( r - 1 ) x r - 2    

Passo 2

Vamos jogar dentro da nossa equação e ver o resultado disso

x 2 y ″ -   3 x y ' +   4 y   =   0 ,

x 2 r ( r - 1 ) x r - 2 - 3 x   r x r - 1 + 4 x r = 0

A sagacidade está em perceber que nossa função y " está sendo multiplicada por x 2 , logo podemos ajustar os expoentes e deixar tudo com a seguinte cara

r ( r - 1 ) x r - 3 r x r + 4 x r = 0

x r ( r r - 1 - 3 r + 4 ) = 0

Logo ou nossa função x r = 0 e assim temos a solução trivial, ou temos a seguinte equação solução

r r - 1 - 3 r + 4 = 0

r 2 - 4 r + 4 = 0

Por produtos notáveis podemos ver que que essa equação pode ser escrita como

r - 2 2 = 0  

Passo 3

Quando temos raízes são iguais, nossa solução tem o seguinte formato:

y = ( c 1 + c 2 ln ⁡ | x | ) x r  

Que no nosso caso fica

y = ( c 1 + c 2 ln ⁡ | x | ) x 2

Passo 4

Vamos descobrir agora as constantes do nosso sistema usando nossos dados de contorno

  y – 1 =   2

  y ' ( – 1 )   =   3  

Com isso nossa solução geral fica

y = ( c 1 + c 2 ln ⁡ | x | ) x 2

2 = c 1  

SHOW!!! Conseguimos o primeiro termo agora vamos usar o segundo dado de contorno para descobrir c 2

y ' = c 2 x x 2 + 2 + c 2 ln ⁡ x 2 x

3 = c 2 - 1 + 2 2 - 1

c 2 =   - 7

Com isso nossa solução fica

y = ( 2 - 7 ln ⁡ | x | ) x 2

Passo 5

Olhando agora para o gráfico da solução, podemos perceber que a solução tendo a zero por que o termo x 2 é mais rápido que a função logaritmo

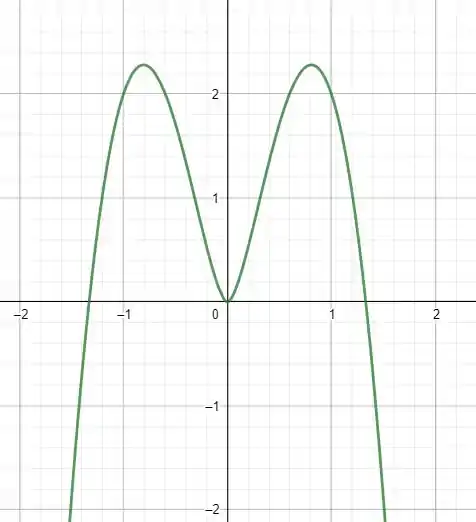
Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

y = ( 2 - 7 ln ⁡ | x | ) x 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

11 - y ' = ( 4 - t y ) / ( 1 + y 2 ) , y 0 = - 2 .
16 - Deduza a fórmula inversa de diferenciação de segunda ordem dada pela Eq. (15)
9 - y ' = t + y , y 0 = 3 .
12 - y ' = ( y 2 + 2 t y ) / ( 3 + t 2 ) , y 0 = 0,5 .
10 - y ' = 2 t + e - t y , y 0 = 1 .