11 - , .
Passo 1
- O problema do valor inicial é:
- A etapa do método Adams-Moulton de quarta ordem é a seguinte:
- Cada etapa do método da diferença inversa de quarta ordem é a seguinte:
, .
Temos então que . Use o método Runge-Kutta para calcular os valores iniciais . Cada etapa do método é dada por:
Onde,
Use o método de previsão e correção de quarta ordem para calcular os valores restantes. O método é dado por:
Para , a fórmula de correção se torna:
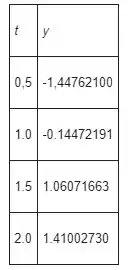
Os valores aproximados dos calculados usando este método com são mostrados na tabela abaixo.
Passo 2
Substituindo a expressão acima por , temos:
Um método para resolver essa equação é usar o método de Newton, que é um método iterativo para encontrar raízes. Vamos então definir uma função.
A aproximação de Euler nos fornece que é a raiz de F. Portanto, uma boa primeira aproximação para é , então vamos supor que . Cada aproximação sucessiva de é calculada com a fórmula abaixa:
A iteração será contínua até que a solução venha a convergir. Para implementar o método de Newton, é necessário conhecer a derivada de :
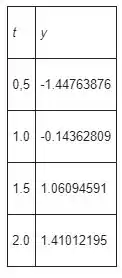
Os valores aproximados dos calculados usando este método com são mostrados na tabela abaixo.
Passo 3
Substituía a expressão por .
Novamente, isso pode ser resolvido usando o método de Newton. Nesse caso, as funções e são:
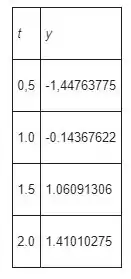
Os valores aproximados dos calculados usando este método com são mostrados na tabela abaixo.
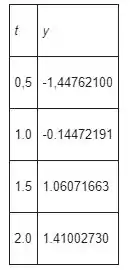
Resposta
a) 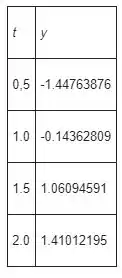
c)