Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.2 - Ex. 11
Em cada um dos problemas de 9 a 20:
(a) Encontre a solução do problema de valor inicial dado em forma explícita.
(b) Desenhe o gráfico da solução.
(c) Determine (pelo menos aproximadamente) o intervalo no qual a solução está definida.
,
Passo 1
- A EDO acima, é do tipo que pode separar para calculcar a solução. A resolução dela é bem parecida com o que fizemos anteriormente em EDO de primeira ordem.
Agora, vamos deixar tudo que tem y de um lado e tudo que tem x do outro lado.
Assim, temos:
Agora para termos uma equação dependendo de y e de x, basta integrar dos dois lados
Integrando dos dois lados, temos:
No enunciado há uma informação de que . Vamos escrever a seguir a solução final que encontramos da EDO.
Ao substituir a informação encontramos o valor da constante C. Logo, temos:
Assim, a equação é:
Passo 2
b)
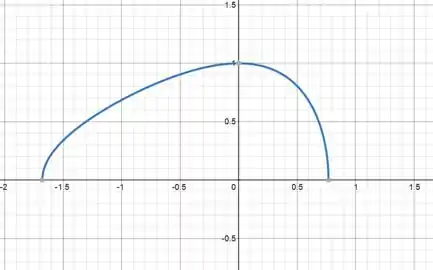
Passo 3
- Temos como equação final da EDO o seguinte:
Assim, temos:
Para saber o intervalo, vamos calcular as raízes da equação, quando y for zero.
Assim, o intervalo em que a dolução está definida é com:
(valor aproximado)
Resposta
Ei, a resposta está no passo a passo :)