Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.6 - Ex. 23
Em cada um dos Problemas 23 e 24:
A - Encontre os Autovalores do sistema dado.
B - Escolha um ponto inicial (diferente da origem) e desenhe as trajetórias correspondentes no plano Desenhe, também, as trajetórias nos planos e
C - Para o ponto inicial do item b desenhe a trajetória correspondente no espaço
23.
Passo 1
A primeira coisa que deve ser feita aqui é determinar a solução desse sistema!
Montando a matriz dos coeficientes baseado no sistema então, obteremos:
Agora devemos buscar os autovalores dela!
Passo 2
AUTOVALORES:
Os autovalores de uma matriz são do tipo:
Onde basicamente o que devemos fazer é subtrair na diagonal principal da matriz , veja:
O determinante de matriz 3x3 é um pouco mais chato que o 2x2. Aqui você tem que repetir as duas primeiras colunas e fazer aquele esquema de multiplicação de diagonais, se lembra?
Simplificando isso aí...
Essa equação só pode ser quando...
Então, se a solução dessa equação é um desses valores aqui:
Onde é o número imaginário .
O conjunto de soluções fundamentais para cada um deles vão ser:
- Para o que é real e único...
- Para que é um número complexo conjugado...
e vem do autovalor complexo:
No nosso caso:
Portanto...
Já e vem do autovetor complexo ( é a parte real e o imaginário). Vamos então determinar todos esses autovetores !
Passo 3
AUTOVETOR 1 - REAL:
Se chamarmos as coordenadas desse vetor de:
Onde , e são os valores das coordenada dele, se os conhecermos então a gente conhece o autovetor! Substituindo ele no lugar de :
Lembre-se de que menos nada mais é do que subtrair da diagonal principal:
Como ...
Resolvendo esse produto matricial aí...
Perceba que e são . Mas o é um número livre pra ser quem ele quiser. Se escolhermos , o autovetor será então...
Passo 4
AUTOVETOR 2 - COMPLEXO:
Agora sim vamos ver quem são aqueles e que te fale ali no passo retrasado! Mas não s e preocupe, a forma de se resolver basicamente é a mesma (a diferença é que são números complexos agora!):
Se chamarmos as coordenadas desse vetor de:
Onde , e são os valores complexos das coordenada dele, se os conhecermos então a gente conhece o autovetor! Substituindo ele no lugar de :
Lembre-se de que menos nada mais é do que subtrair da diagonal principal:
Como (por vias de cálculo, podemos trabalhar apenas com o lado positivo, oi seja, )...
Resolvendo esse produto matricial aí...
Da última equação...
Da segunda ou da primeira...
E agora escolher algum valor para , tipo , perceba que . Então...
Ou seja...
Separando esse vetor em parte real e parte complexa...
A parte real é o :
Já a parte imaginária...
Passo 5
Logo, as três soluções fundamentais serão:
Substituindo...
A solução final é então dada pela expressão:
Passo 6
Beleza! Então com isso a gente tem a solução do nosso problema. Para resolver a letra de fato, precisamos chutar uma condição inicial para então desenhar nos planos as curvas.
Não podemos chutar a origem, mas que tal:
Assim...
Então, como , enquanto o seno de é e o cosseno ...
Ou seja, a solução para o nosso ponto inicial é:
Passo 7
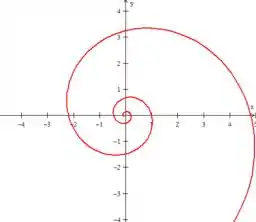
Se usarmos um software de gráfico para desenhar essas curvas paramétricas aí, no plano , ou como o exercício chamou, vamos obter...
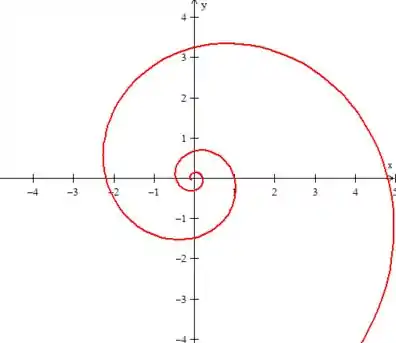
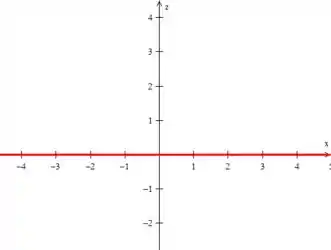
Já no plano , como duranto todo o , é como se olhássemos de lado para uma folha de papel: só veríamos uma reta no :
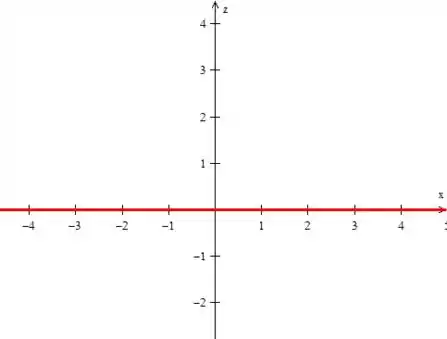
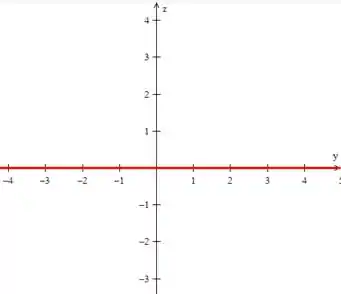
O mesmo vai ser no plano :
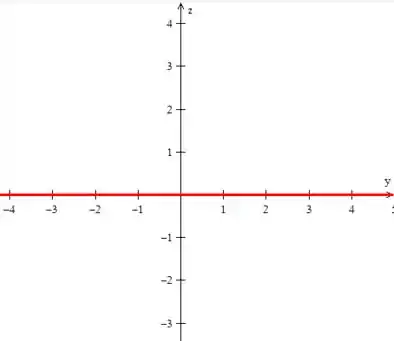
Passo 8
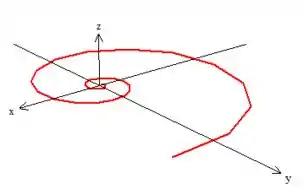
Se a gente juntar mentalmente essas três figuras o que você acha que vai dar? Faça essa pergunta para treinar a sua visão em 3D . Aqui vai a resposta:
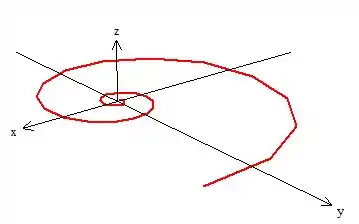
Resposta
Letra A:
Letra B:
Letra C:
