Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.6 - Ex. 14
Em cada um dos problemas de 13 a 20, a matriz de coeficientes contém um parâmetro α. Em cada um desses problemas:
(a) Determine os autovalores em função de α.
(b) Encontre o valor ou valores críticos de α em que muda a natureza qualitativa do retrato de fase para o sistema.
(c) Desenhe retratos de fase para um valor de α ligeiramente menor, e para outro valor ligeiramente maior, do que cada valor crítico.
Passo 1
Fazendo a determinante abaixo nós encontraremos os autovalores:
E as raízes dessa equação serão:
Passo 2
Para termos raízes reais e iguais nós precisamos ter:
Dois valores bons para teste são
E para termos raízes complexas precisaremos ter:
E com isso vamos testar três valores e só para ver mesmo.
Passo 3
Para temos:
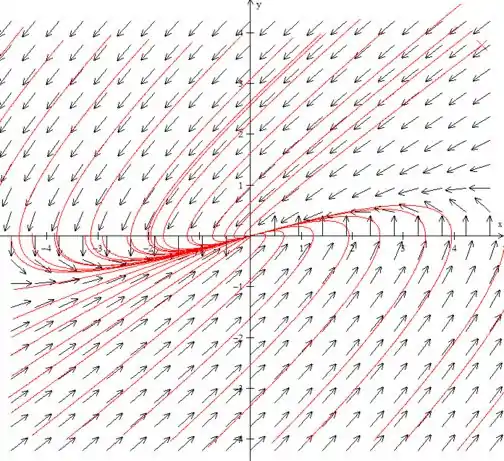
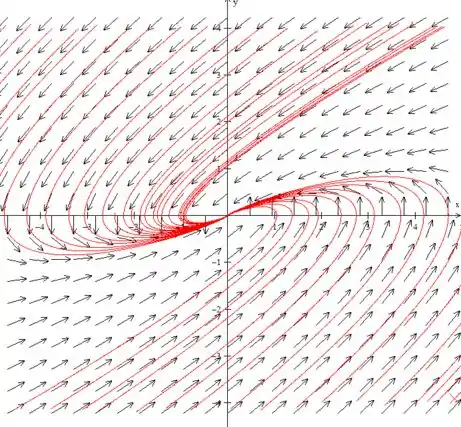
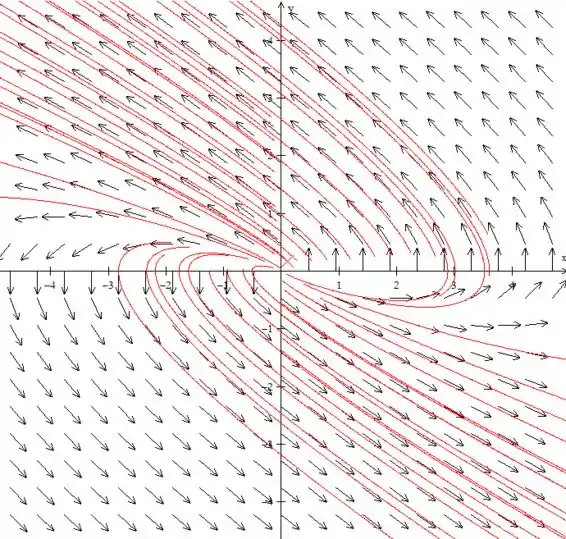
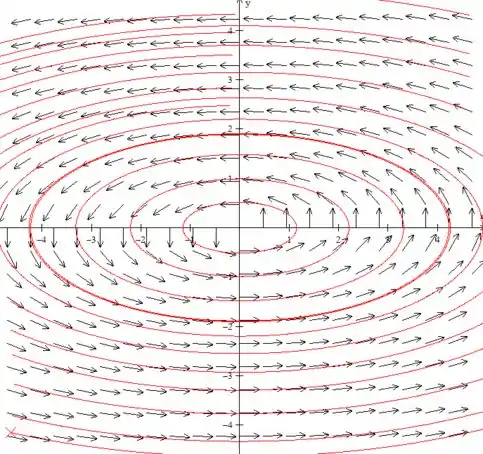
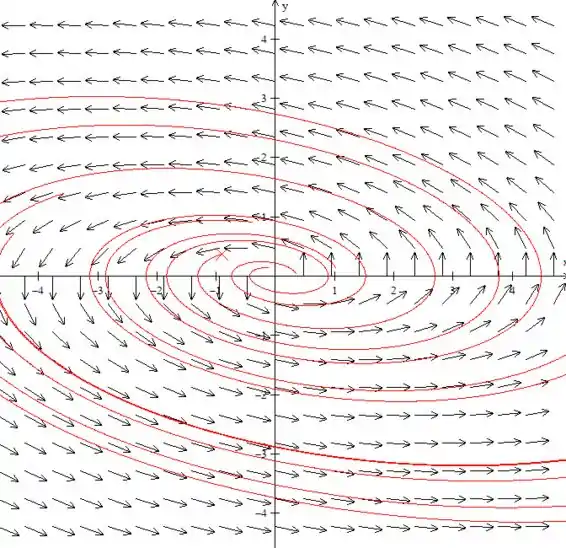
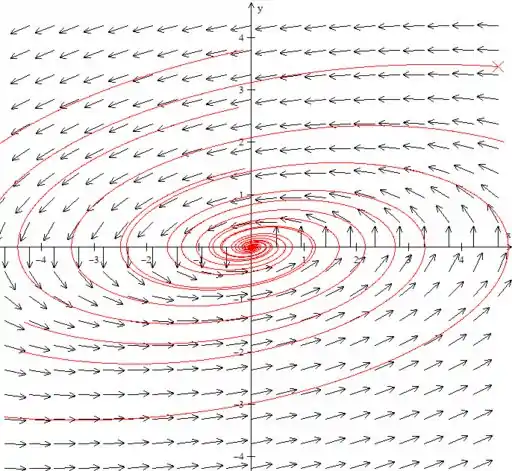
Acho que já deu para entender hahaha
Resposta
Exercícios de Livros Relacionados
Em cada um dos problemas de 1 a 4:(a) Desenhe um campo de direções e esboce algumas trajetórias.(b) Descreva como as soluções se comportam quando t→∞ .(c) Encontre a solução geral do sistema de equaçõ
Considere, novamente, o circuito elétrico no Problema 26 da Seção 7.6. Esse circuito édescrito pelo sistema de equações diferenciais: d d t I V = 0 1 L - 1 C - 1 R C I V a)Mostre que os autovalores sã
Considere novamente o sistema x ' = A x = 1 - 1 1 3 x que discutimos no Exemplo 2. Vimos que A tem um autovalor duplo r 1=r 2=2 com um único autovetor independente ξ 1=1 ,- 1 T ou qualquer múltiplo de
Seja J = λ 1 0 0 λ 1 0 0 λ Em que 1 é um numero real arbitrário.b)Use um argumento indutivo para mostrar que: J n = λ n n λ n - 1 n n - 1 2 λ n - 2 0 λ n n λ n - 1 0 0 λ n
Considere o sistema x ' = A x = 1 1 1 2 1 - 1 - 3 2 4 x (e) Escreva uma matriz fundamental Ψ ( t ) para o sistema (i).