Em cada um dos problemas de 13 a 20, a matriz de coeficientes contém um parâmetro α. Em cada um desses problemas:

(a) Determine os autovalores em função de α.

(b) Encontre o valor ou valores críticos de α em que muda a natureza qualitativa do retrato de fase para o sistema.

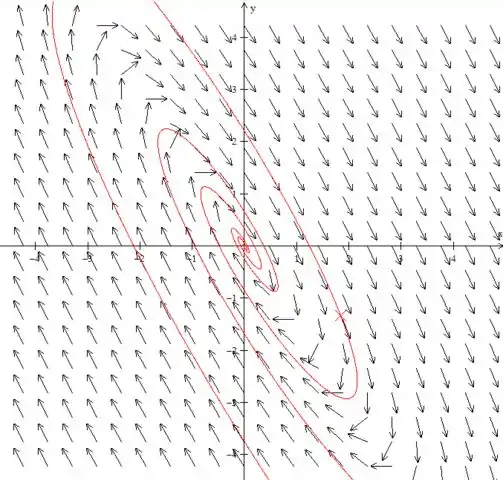
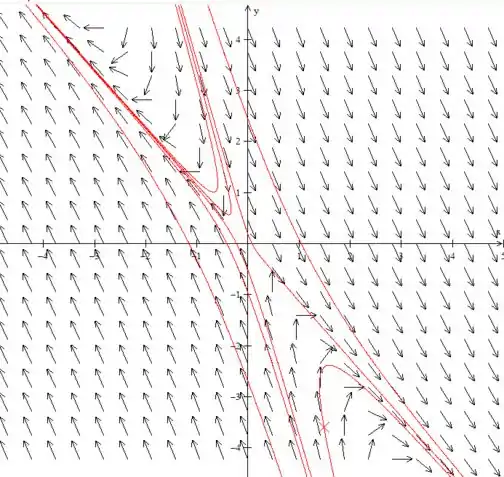
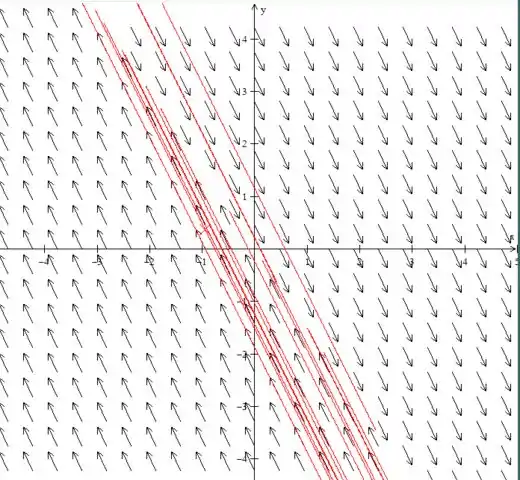
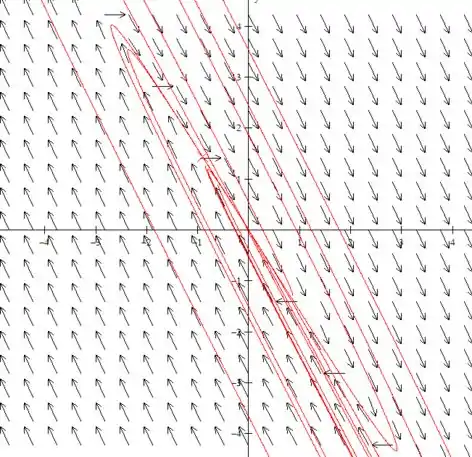
(c) Desenhe retratos de fase para um valor de α ligeiramente menor, e para outro valor ligeiramente maior, do que cada valor crítico.

Tirando os autovetores desse sistema teremos:

Tirando Bhaskara nessa equação do segundo grau teremos:

Esse sistema será oscilante se:

Ou seja:

E será um sistema estável, pois a parte real é negativa.

Então para temos autovalores reais e diferentes.

E esse sistema começará a ser instável quando:

Isso quer dizer que há um intervalo entre e onde o sistema ainda é estável e não é oscilante.