Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.6 - Ex. 12

Em cada um dos Problemas 11 e 12:

(a) Encontre os autovalores do sistema dado.

(b) Escolha um ponto inicial (diferente da origem) e desenhe a trajetória correspondente no plano x 1 x 2 .

(c) Para a sua trajetória encontrada em (b), desenhe os gráficos de x 1 e x 2 em função de t .

(d) Para a sua trajetória encontrada em (b), desenhe o gráfico correspondente no espaço tridimensional t x 1 x 2 .

x ' = - 4 / 5 2 - 1 6 / 5 x

Passo 1

Os autovalores do sistema serão:

d e t - 4 5 - r 2 - 1 6 5 - r = 0

Esse será:

- 4 5 - r 6 5 - r + 2 = 0

r 2 + 4 5 - 6 5 r - 24 2 5 + 2 = 0

r 2 - 2 5 r + 26 2 5 = 0

E as raízes dessa equação serão:

r 1 ; r 2 = + 1 5 ± 4 25 - 4 × 26 25 2

r 1 ; r 2 = 1 5 ± i

Passo 2

Pegando o autovalor r = 1 5 - i nós teremos um autovetor igual a:

- 4 5 - 1 5 + i 2 - 1 6 5 - 1 5 + i ξ 1 1 ξ 2 1 = 0

- 1 + i 2 - 1 1 + i ξ 1 1 ξ 2 1 = 0

Então pela segunda linha dessa matriz nós teremos:

ξ 1 1 = 1 + i ξ 2 1

Nos dando um autovetor igual a:

ξ 1 = 1 + i 1

Então a solução desse sistema será:

x 1 = 1 + i 1 e t 5   e - i t = 1 + i 1 e t 5   cos ⁡ t - i s e n   t

x 1 = e t 5   cos ⁡ t + s e n   t cos ⁡ t + i e t 5 - s e n   t + cos ⁡ t - s e n   t

E a solução geral será igual a:

x = c 1 e t 5   cos ⁡ t + s e n   t cos ⁡ t + c 2 e t 5 - s e n   t + cos ⁡ t - s e n   t

Passo 3

Vamos considerar que o ponto inicial será x 1 = a e x 2 = b (mais tarde vamos colocar um ponto qualquer) e com isso nossas constantes serão:

a = c 1 + c 2

b = c 1

Logo:

c 2 = a - b

Logo a equação de x será:

x = e t 5 b   cos ⁡ t + s e n t + ( a - b ) ( - s e n   t + cos ⁡ t ) a cos ⁡ t - a - b s e n   t

x = e t 5 2 b   s e n   t - a   s e n   t + a cos ⁡ t a cos ⁡ t - a - b s e n   t

Passo 4

Então para o ponto inicial ( 1,1 ) ou seja a = b = 1 nós teremos a seguinte trajetória:

Passo 5

E como calculamos a equação de x 1 e x 2 no passo 3 sem os valores de a e b , então se substituirmos nós teremos:

x = x 1 x 2 = e t 5   s e n   t + cos ⁡ t cos ⁡ t

O que vai nos dar os seguintes gráficos:

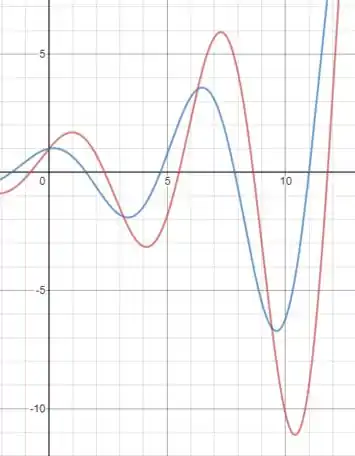
Com o gráfico azul sendo x 2 e o vermelho x 1 .

Passo 6

Já para a letra d

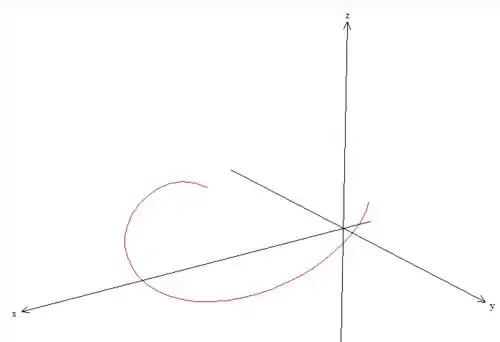
Considerando :

x = t

y = x 1

z = x 2

Resposta

a ) r 1 ; r 2 = - 1 5 ± i

b )   I m a g e m   d o   p a s s o   4

c )   I m a g e m   d o   p a s s o   5

d )   I m a g e m   d o   p a s s o   6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o sistema x ' = A x = 1 1 1 2 1 - 1 - 3 2 4 x a)Mostre que r = 2 é um autovalor de multiplicidade 3 da matriz de confiecnetes A e que existe apenas um autovetor independe associado, a saber,
Considere o sistema x ' = A x = 5 - 3 - 2 8 - 5 - 4 - 4 3 3 x b) Para encontrar uma terceira solução, suponha que x=ξ t e t+η e t ; mostre que, então, ξ e η têm que satisfazer A - I ξ = 0 A - I η = ξ
Considere o sistema x ' = A x = 5 - 3 - 2 8 - 5 - 4 - 4 3 3 x a) Mostre que r = 1 é um autovalor triplo da matriz de coeficientes A e que existem dois autovetores associados lineramente indepednetes,
Considere o sistema x ' = A x = 1 1 1 2 1 - 1 - 3 2 4 x f) Forme a matriz T com o autovetor ξ 1 na primeira coluna e os autovetores generalizados η e ζ na segunda e terceira colunas. Depois, encontre
Considere o sistema x ' = A x = 5 - 3 - 2 8 - 5 - 4 - 4 3 3 x e) Escreva uma matriz fundamental Ψ ( t ) para o sistema (i).