Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 5.2 - Ex. 23
Em cada um dos problemas de 23 a 28, faça o gráfico de diversas somas parciais da solução em série do problema de valor inicial dado em torno de x = 0, obtendo, assim, gráficos análogos aos ilustrados nas Figuras de 5.2.1 a 5.2.4.
Passo 1
Tá legal! Conforme dito no enunciado, vamos buscar a solução do Problema 23 lá no Problema 2, que já foi resolvido, então, teremos:
Passo 2
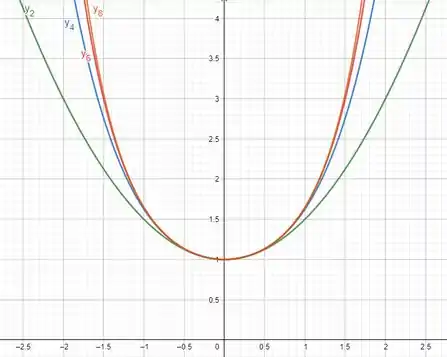
Agora com a solução em mãos, ficou fácil plotar os gráficos das somas parciais. O gráfico é apresentado a seguir:
Resposta
Exercícios de Livros Relacionados
Nos problemas 21-30, resolva cada equação diferencial da maneira dos capítulos anteriores e então compare os resultados com as soluções obtidas através de séries de potências y = ∑ n = 0 ∞ x n . x n (
Nos problemas 21-30, resolva cada equação diferencial da maneira dos capítulos anteriores e então compare os resultados com as soluções obtidas através de séries de potências y = ∑ n = 0 ∞ x n . x n y
Nos problemas 21-30, resolva cada equação diferencial da maneira dos capítulos anteriores e então compare os resultados com as soluções obtidas através de séries de potências y = ∑ n = 0 ∞ x n . x n (
Nos problemas 21-30, resolva cada equação diferencial da maneira dos capítulos anteriores e então compare os resultados com as soluções obtidas através de séries de potências y = ∑ n = 0 ∞ x n . x n y
Nos problemas 21-30, resolva cada equação diferencial da maneira dos capítulos anteriores e então compare os resultados com as soluções obtidas através de séries de potências y = ∑ n = 0 ∞ x n . x n 2