Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.6 - Ex. 3
Em cada um dos problemas de a :
Expresse a solução geral do sistema de equações dado como combinação e de funções reais
Desenhe, também um campo de direções, esboce algumas trajetórias e descreva o comportamento das soluções quando
Passo 1
Calculando os autovalores dessa matriz nós iremos obter:
Dessa vez temos uma solução puramente imaginária, ou seja, nós teremos algo do tipo:
Passo 2
O autovetor para será:
Fazendo a multiplicação matricial nós teremos:
Se colocarmos e nós solucionaremos os dois casos. Então nosso autovetor será:
Portanto a solução do sistema se dará fazendo:
E a solução geral será na forma de:
Se fizermos a solução com o autovalor estaríamos certos também.
Passo 3
O campo de direções desse sistema seria:
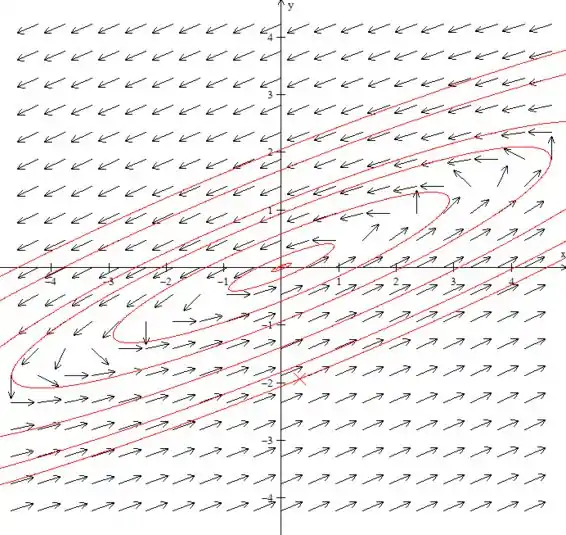
E como essa função forma uma espiral fechada então não dá para dizer o que acontece quando . Pois ele será uma função alternada.