Considere o sistema
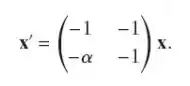
Resolva o sistema para . Quais são os autovalores da matriz de coeficientes? Classifique o ponto de equilíbrio na origem em relação ao tipo.
Resolva o sistema para . Quais são os autovalores da matriz de coeficientes? Classifique o ponto de equilíbrio na origem em relação ao tipo.
As soluções encontradas em e exibem dois tipos de comportamento bem diferentes. Encontre os autovalores da matriz de coeficientes em função de e determine o valor de entre e em que ocorre a transição de um tipo de comportamento para outro.
Passo 1
Cara, vamos começar pela ? Pois ela é a parte teórica disso e com ela já matamos a questão de fato e qualquer dúvida em relação a essa matéria.
Os autovalores desse sistema serão iguais a:
Fazendo por Bháskara nós temos:
Passo 2
Calculando o auto vetor para esses dois resultados de autovalor que encontramos nós temos:
Para teremos o autovetor :
Fazendo a multiplicação vetorial teremos:
Portanto o autovalor para será:
Portanto a solução para esse autovalor será:
Passo 3
Agora para teremos um autovetor igual a :
Fazendo a multiplicação vetorial teremos:
Nos dando um autovetor igual a:
Portanto a solução será igual a:
Nos dando uma solução geral igual a:
Passo 4
Por hora cara, vamos dizer que e e vamos escrever e de .
E pelo autovalor vemos que ocorre uma transição em
Pois quando temos uma função constante. Então para teremos um comportamento de e de parecido com:
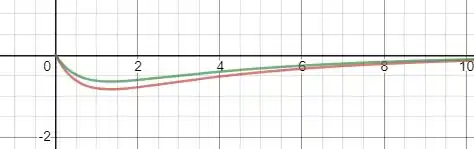
Caracterizando em um sistema estável ( é a curva vermelha e a verde)
Agora para para teremos:
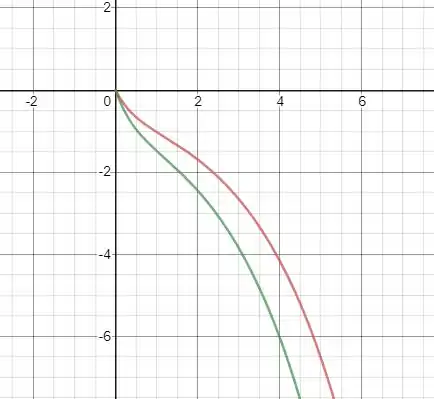
O que caracteriza em um sistema instável.
A página para encontrar esses dois comportamentos estarão disponíveis em
https://www.desmos.com/calculator/nkozknv4vh
Basta variar
Passo 5
Depois de ter matado a cobra e ter mostrado o pau que a matou vamos responder as questão.
Os autovalores que encontramos valem:
Quando teremos:
O que caracteriza em um sistema instável.
Plotando o campo de direções do sistema nós teremos:
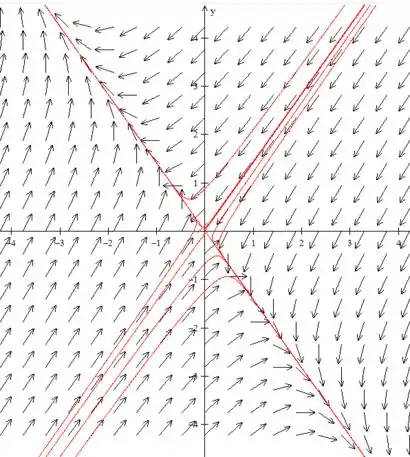
Passo 6
Já para teremos autovalores iguais a:
O que caracteriza em uma sistema estável. Plotando o campo de vetores nós temos:
