Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.5 - Ex. 25
Em cada um dos problemas de a , são dados os autovalores e autovetores de uma matriz . Considere o sistema correspondente .
Esboce um retrato de fase do sistema
Esboce a trajetória que contém o ponto inicial
Para a trajetória no item . Esboce os gráficos de e de em função de no mesmo conjunto de eixos.
Passo 1
Seguindo o mesmo raciocínio que fizemos na questão anterior nós temos que a matriz será entendida como:
E pelos autovalores e autovetores temos que a matriz será igual a:
Fazendo as duas multiplicações vetoriais teremos:
Comparando a primeira com a terceira e a segunda com a quarta nós teremos:
Deixando nossa matriz como:
Isso deixa nosso retrato de fase igual a:
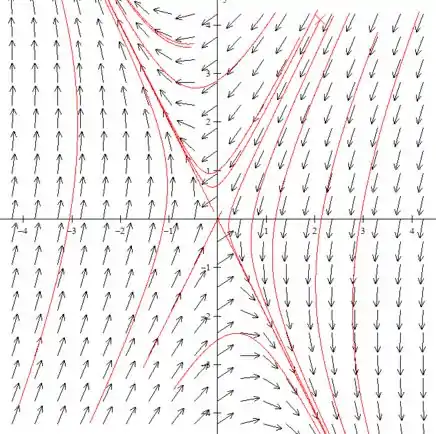
O que caracteriza em um sistema instável.
Passo 2
Como em a região está decrescendo então ficaremos com a imagem do ponto até em baixo de forma que:
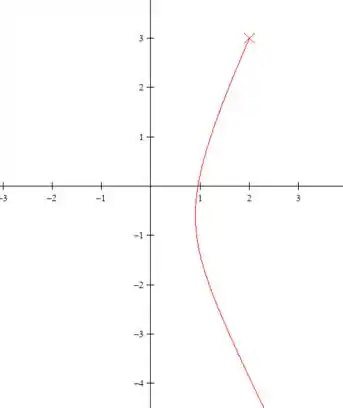
Onde é a horizontal e a vertical.
Passo 3
A equação que correlaciona e com o tempo é dada por:
Aplicando a condição inicial com e nós teremos:
Então:
Deixando nossa equação como:
E plotando as duas funções nós teremos:
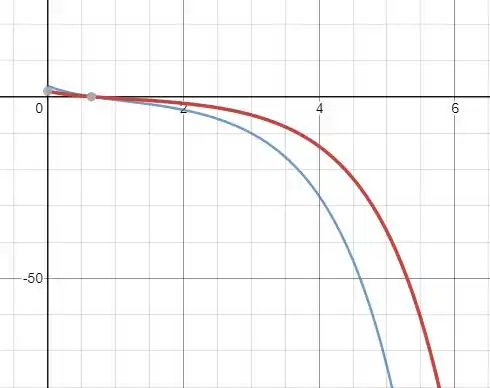
As duas funções tendem a .