Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.6 - Ex. 13
Em cada um dos problemas de 13 a 20, a matriz de coeficientes contém um parâmetro α. Em cada um desses problemas:
(a) Determine os autovalores em função de α.
(b) Encontre o valor ou valores críticos de α em que muda a natureza qualitativa do retrato de fase para o sistema.
(c) Desenhe retratos de fase para um valor de α ligeiramente menor, e para outro valor ligeiramente maior, do que cada valor crítico.
Passo 1
Encontrando os autovalores dessa matriz nós teremos:
E as raízes dessa equação do segundo grau serão:
Passo 2
A estabilidade depende do valor real do autovalor, ou seja quando nós teremos um termo exponencial igual a:
Sendo um sistema instável.
E quando teremos:
Caracterizando em um sistema estável.
Passo 3
Quando é negativo teremos algo como:
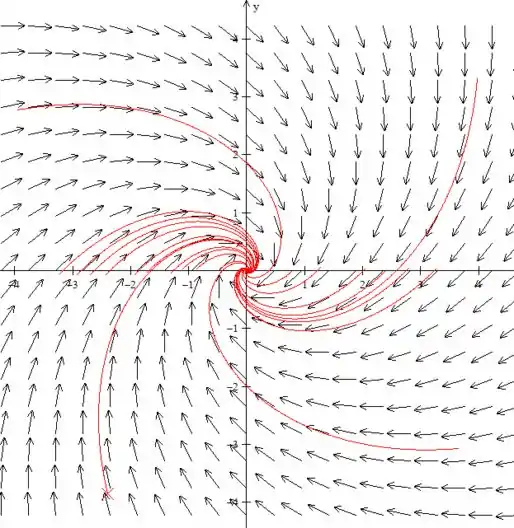
Onde todos os valores convergem na origem (no exemplo colocamos )
Agora quando teremos:
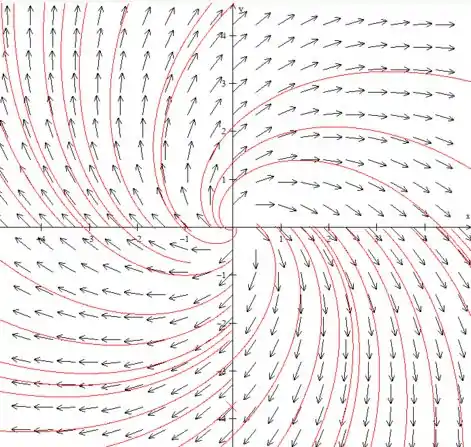
Onde todos os valores vão para infinito. (no exemplo colocamos )