Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.8 - Ex. 12
Em cada um dos Problemas 11 e 12, seja e use o método das aproximações sucessivas para aproximar a solução do problema de valor inicial dado.
- Calcule ou (se necessário) aproximações de Taylor desses iterados. Mantenha termos até a sexta ordem.
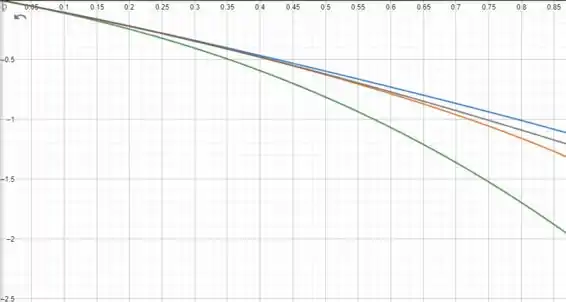
- Faça o gráfico das funções encontradas em (a) e observe se elas parecem estar convergindo.
Passo 1
Nesse exercício, vamos usar o método das aproximações sucessivas, como visto no capítulo, com as integrais e, caso necessário, aproximações de Taylor para encontrar as funções . Vamos resolver juntos!!
Passo 2
- Bom, vamos lá! Temos que a função que nos mostra como fazer as aproximações sucessivas é definida por
Substituindo nossa função na integral, ficamos com
Temos ainda que , que é uma aproximação de Taylor. Substituindo, teremos
Agora para , nossas primeiras quatro aproximações, com o auxilio computacional, se tornam
Passo 3
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Considere a sequência ϕ n x = 2 n x e - n x 2 ,0 ≤ x ≤ 1 .Mostre que lim n → ∞ ϕ x = 0 para 0 ≤ x ≤ 1 ; logo, ∫ 0 1 lim n → ∞ ϕ n d x = 0 Mostre ∫ 0 1 2 n x e - n x 2 d x = 1 - e - n ; então, ∫ 0
Nos problemas de 15 a 18, indicamos como provar que a sequência ϕ n t , definida pelas equações de (4) a (7), converge.Note que ϕ n t = ϕ 1 t + ϕ 2 t - ϕ 1 t + … + ϕ n t - ϕ n - 1 t . Mostre que ϕ n t
Nos problemas de 15 a 18, indicamos como provar que a sequência ϕ n t , definida pelas equações de (4) a (7), converge.Se ∂ f / ∂ y for contínua no retângulo D , mostre que existirá uma constante posi
Nos problemas de 15 a 18, indicamos como provar que a sequência ϕ n t , definida pelas equações de (4) a (7), converge.Mostre que, se t ≤ h , então ϕ 1 t ≤ M t ,em que M é escolhido de modo que f t ,