Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.2 - Ex. 53
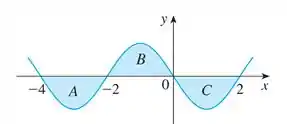
Cada uma das regiões A, B, C delimitadas pelo gráfico de e o eixo tem área 3. Encontre o valor de
Passo 1
Olá amigo, Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui temos que calcular a integral dada que é
Para isso devemos analisar o gráfico da função
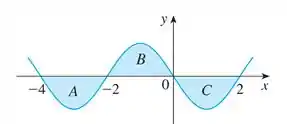
e utilizar o conceito de área sob a curva de uma integral para conseguirmos resolver a atividade.
Vale relembrar que uma integração de em um intervalo significa a área de abaixo da curva no intervalo dado.
Passo 2
Vamos chamar
Podemos reescrever como a soma de integrais de cada função:
Vamos resolver cada um separadamente.
corresponde a área resultante delimitada por e o eixo do gráfico mostrado:
Se traçarmos a reta , temos que corresponde a área do triângulo formado por essa reta:
Se traçarmos a reta , corresponde a área do retângulo formado:
Então, temos:
Resposta