Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.2 - Ex. 14
Com uma calculadora programável ou computador (veja as instruções para exercício 9 da seção 5.1) , calcule as somas de Riemann esquerda e direita para a função no intervalo , com . Explique por que as estimativas mostram que
Passo 1
Bom pessoal, nessa questão temos que resolver a soma de Riemann para a seguinte função:
No intervalo de até . Faremos a soma a direita e a esquerda, usando um número de subintervalos .Para isso, podemos usar uma calculadora programável, portanto, não precisamos de fato fazer as contas aqui.
Lembrando o que a soma de Riemann representa:
Ela é o cálculo da área de retângulos que são feitos em subintervalos do intervalo total. A altura do retângulo é o valor da função em um ponto do subintervalo e a base do retângulo é o comprimento do subintervalo, de forma que temos o seguinte somatório:
Com
Onde é o número de subintervalos. é o comprimento de cada subintervalo e são os extremos do intervalo total.
é um valor de que pertence ao subintervalo. Na soma a direita, esse valor é escolhido como sendo o extremo direito do subintervalo e na soma a esquerda, esse valor é escolhido como sendo o extremo esquerdo do subintervalo.
Por fim, teremos que explicar por que que:
Bora lá?
Passo 2
Vamos fazer a soma de Riemann a esquerda. Usando uma calculadora programável e um software gráfico, temos o seguinte resultado:
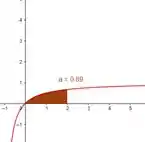
(Como temos um número muito grande de subintervalo , não dá nem pra ver esses retângulos, mas eles estão ali, pode acreditar.)
Pela esquerda, tivemos portanto o resultado:
Já pela direita, temos o seguinte resultado:
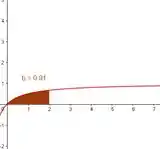
Todos os valores expressos na figura estão arredondados pelo computador.
Mas a condição que nos foi dada é sempre verdadeira, pois a área não é menor que 0,9 e não maior, então as somas tendem a ficar próximos o valor real.
Como podemos ver no gráfico, a função é crescente no intervalo dado.Dessa forma, uma soma de Riemann pela direita representa uma superestimativa para a área.
Enquanto, que uma soma de Riemann pela esquerda para uma função crescente representa uma subestimativa para a área.
E como a integral nada mais é do que essa área, vamos ter, portanto, que:
Vou colocar aqui uma função crescente e uma estimativa pela direita para provar que ela nos dá uma superestimativa:
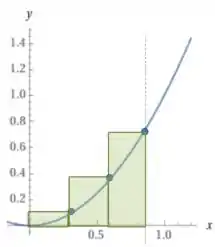
E uma soma pela esquerda para provar que ela nos dá uma subestimativa:
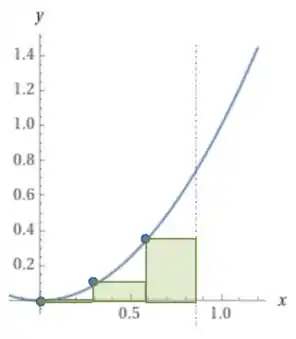
E isso é válido para toda função crescente no intervalo.
Resposta
Como a função é crescente, temos que a soma pela esquerda é uma subestimativa para a área e a soma pela direita é uma superestimativa para a área. E como a área é dada pela integral, temos portanto que:
Os valores diferem dos dados no enunciado por conta da aproximação realizada pelo calculadora programável usada.