Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 24
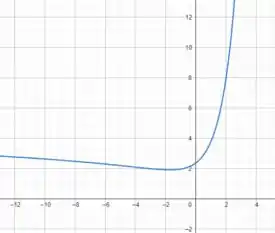
Faça o gráfico da função usando quantas visualizações retangulares você precisar para descrever a verdadeira natureza da função.
Passo 1
Nesse problema foi dada a função
E nosso objetivo é plotar o gráfico de usando uma visualização retangular que descreva a natureza real dessa função.
Parece complicado?
Para resolver esse problema temos que usar uma ferramenta gráfica para plotar o gráfico da função e a partir daí vamos analisar qual é o melhor intervalo que podemos plotar essa função para podermos ter uma real noção do seu comportamento.
Saca só!
Passo 2
Quando plotamos o gráfico de podemos perceber que seu comportamento é bem simples... como e são funções cujos gráficos são “comportados”, podemos plotar em uma única janela.
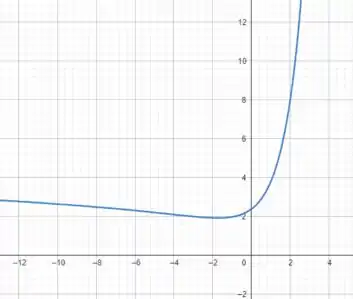
Observamos que ela possui uma assíntota vertical em e possui ponto de mínimo em
. Além disso ela cresce de e decresce de .
É isso! O que achou? Responde Aí!
Resposta
