Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.6 - Ex. 24

24. Calcular ∬ R e x 2 d y   d x   onde R é a região descrita na figura 7.20.

Passo 1

Temos que a representação gráfica é a seguinte:

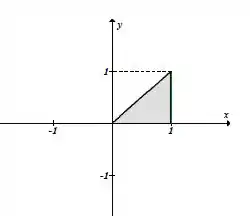
Analisando o gráfico, temos a seguinte integral de acordo com os limites encontrados:

∫ 0 1 ∫ 0 x   e x 2   d y   d x

Vamos integrar em relação a y primeiro,

∫ 0 x e x 2 d y =

e x 2 y 0 x = 1 2 e x 2

Passo 2

∫ 0 1 1 2 e x 2     d x =

1 2 e x 2   0 1 =

1 2 e - 1 2

Resposta

1 2 e - 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral dupla. ∬ D e y 2 d A , D = { ( x , y ) | 0 ≤ y ≤ 1 ,0 ≤ x ≤ y }
Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
9. Calcular ∬ R ( x 2 + y 2 )d x d y , onde R é a região delimitada por y = xex = 4ey = 0 .
10. Calcular ∬ R d yd x x + y 2, onde R é o retângulo 3 ≤ x ≤ 4 e 1 ≤ y ≤ 2 .
8. Calcular ∬ R y l nx xd y d x , onde R é o retângulo 1 ≤ x ≤ 2 e - 1 ≤ y ≤ 1 .