Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 7.6 - Ex. 25

Calcular a área da região limitada pelas curvas

y = (1)/((x - 1) (x - 4)) , y = (1)/((1 - x) (x - 4)) , x = 2 e x = 3 .

Passo 1

Eu vou chamar (1)/((x - 1) (x - 4)) de y 1 e (1)/((x - 1) (x - 4)) de y 2 pra não confundir na hora de montar.

A área que a gente quer é a dessa figura aqui:

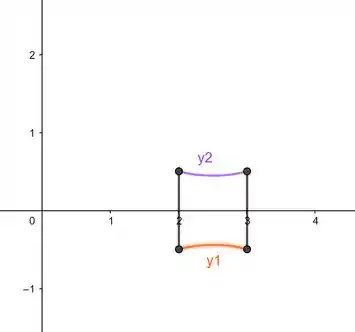
Passo 2

Então, como a gente sabe, temos que calcular a integral assim:

int_2^3 (1)/((1 - x) (x - 4)) - (1)/((x - 1) (x - 4)) d x

Aí a gente pode fazer:

int_2^3 (- 1)/((x - 1) (x - 4)) - (1)/((x - 1) (x - 4)) d x

int_2^3 - (2)/((x - 1) (x - 4)) d x

Agora a gente tem que calcular essa integral usando frações parciais. São termos lineares, então vai ficar assim:

- (2)/((x - 1) (x - 4)) = (A)/(x - 1) + (B)/(x - 4)

Vamos achar A e B agora...

Passo 3

Desenvolvendo ali vai ficar sim:

- (2)/((x - 1) (x - 4)) = (A ( x - 4 ))/(x - 1) + (B ( x - 1 ))/(x - 4)

Vamos cortar os denominadores agora...

- 2 = A (x - 4) + B ( x - 1 )

- 2 = A x - 4 A + B x - B

- 2 = x (A + B) - 4 A - B

Pra isso ser igual, a gente precisa que:

{[[A + B = 0],[- 4 A - B = - 2]])

Aí a gente tem que A = - B , então:

4 B - B = - 2 -> B = - (2)/(3)

E A = (2)/(3) .

Passo 4

Vamos remontar a integral agora com esses valores:

I = int_2^3 (2)/(3 (x - 1)) - (2)/((x - 4)) d x

A gente separa em duas:

= (2)/(3) [int_2^3 (1)/(x - 1) d x - int_2^3 (1)/(x - 4) d x]

Integrando a gente fica com:

= (2)/(3) [ln |x - 1| - ln |x - 4|]_2^3

= (2)/(3) [ln |3 - 1| - ln |3 - 4| - ln |2 - 1| + ln |2 - 4|]

= (2)/(3) [ln 2 - ln 1 - ln 1 + ln 2]

= (2)/(3) (2 ln 2)

(4 ln 2)/(3) u . a

Essa é a área procurada😉

Resposta

(4 ln 2)/(3) u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral.int (d s)/(s^2 (s - 1)^2)
Calcule a integral.int (x^2 - 2 x - 1)/((x - 1)^2 ( x^2 + 1 )) d x
Calcule a integral.int_3^4 (x^3 - 2 x^2 - 4)/(x^3 - 2 x^2) d x